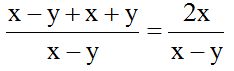Operations with Algebraic Fractions
Adding and subtracting algebraic fractions:
10.1 Calculate the result of the sum:
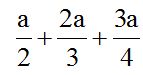
1st. Calculate the least common multiple (l.c.m.) of the denominators: We find that the l.c.m.(2, 3, 4) = 12
2nd. Divide the l.c.m. by each denominator (the value below the fraction), then, multiply the quotient times the numerator (the value above the fraction):
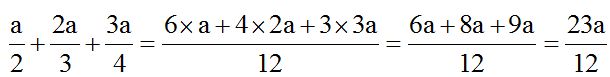
10.2 Calculate the value of:
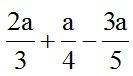Answer: 
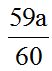Solution: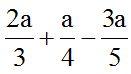 
1st. Calculate the l.c.m. (3, 4 and 5) = 60
2nd. Divide 60 by each denominator, then, multiply the quotient times the numerator. Write its corresponding sign in front.
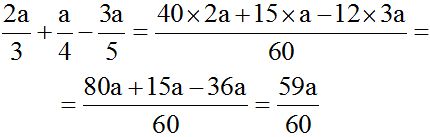
10.3 Calculate the sum:
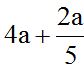Answer: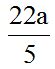 
Solution:
When you find a whole number (no denominator), you can use 1 as a denominator to make things easier. Dividing or multiplying a number by 1 results in the same number, but it sometimes clears any doubts:
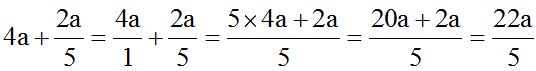
The l.c.m. of the denominators is 5. Each denominator is divided by this number, then, multiply the quotient times the numerator.
10.4 Calculate:
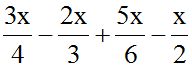Answer: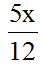 
10.5 Calculate:
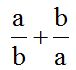Answer: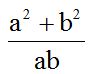 
Solution:
Working with letter variables is simple. The l.c.m. of ‘a’ and ‘b’ is ‘ab’. These two letter variables have nothing in common. Imagine that ‘a’ is equal to 7 and ‘b’ is equal to 5. Since 7 and 5 are prime numbers, they have nothing in common, their l.c.m.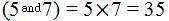 
is the same as the l.c.m.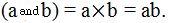 
Each denominator is divided by this number, then, we multiply the quotient times the numerator:
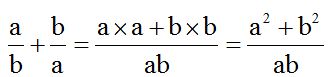
Dividing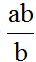 
is like dividing
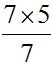imagining that 'a' = 7 and 'b' = 5.
We simplify the equal factors in the numerator and denominator and we will get:
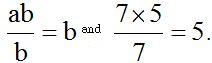
10.6 Calculate:
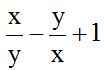Answer: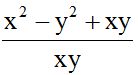 
Solution:
This exercise can be written like this:
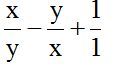
The l.c.m. of the denominators is 'xy'
We divide this value by each denominator, then, multiply the quotient times the numerator:
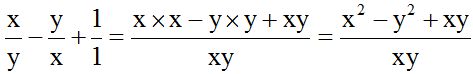
We mustn't simplify the xy in the numerator with the xy in the denominator because the numerator is adding. To be able to simplify terms, they need to be multiplying.
10.7 Calculate the sum:
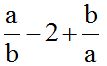Answer: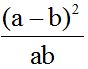 
Solution:
The l.c.m. of these denominators is ‘ab’. We divide this value by each denominator, then, multiply the quotient times the numerator:
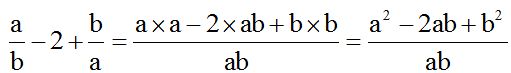
We find that the numerator is the square of the difference between both numbers:
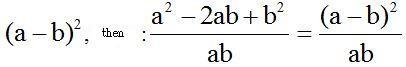
10.8 Calculate:
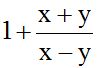Answer: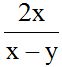 
Solution:
The denominator for both will be (x – y).
We multiply the numerator 1 by (x – y). I multiply the second numerator by 1 because (x – y) divided by itself equals 1:
Solution:
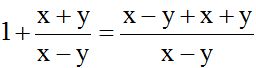
I simplify (reduce) similar terms in the numerator:
