How do we Rationalize a Denominator Which is Composed by both Positive and Negative Signs?
Imagine we must rationalize:
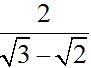
To rationalize the denominator of a fraction composed by a binomial, we need to multiply the numerator and denominator of the fraction times the conjugate of the denominator.
What is a binomial conjugate?
A binomial conjugate is another binomial similar to the first but the sign of the second term is the opposite than it previously had:
Examples:
The conjugate of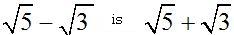 
The conjugate of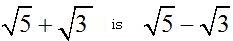 
The conjugate of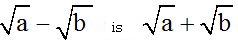 
Remember: the sum of two numbers by their difference is equal to the difference of their squares.
The square of any quantity in a square root results in removing the radical and keeping the radicant: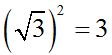 
If the numerator and denominator of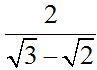 
are multiplied by their conjugate, which is
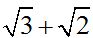, I would get the difference of their squares in the denominator, 3 – 2 = 1:
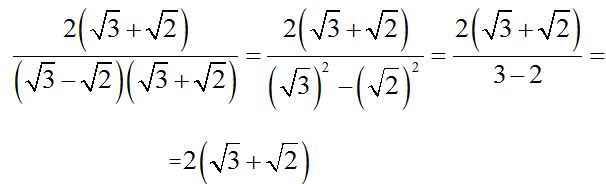
Remember that if I multiply or divide both terms in a fraction by the same number, the value of the fraction doesn't vary.
10.83 Calculate:
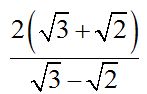Answer: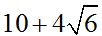 
Solution:
We multiply the numerator and denominator by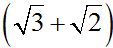 
.
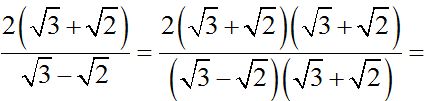
We see that in the numerator we have the square of the sum of two numbers:
.
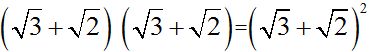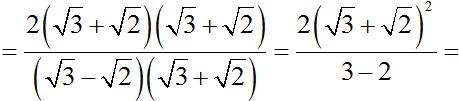
We know that the square of the sum of two numbers is equal to:
the square of the first: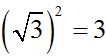 
,
plus two times the first by the second: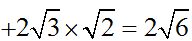 
,
plus the square of the second: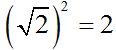 
,
which is what you have next: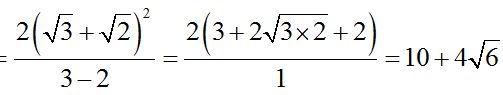
10.84 Calculate:
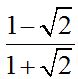Answer: 
.
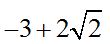Solution:
We see numbers without square roots in the numerator and denominator. The procedure is the same because, in order to eliminate square roots in the denominator, we need to have square differences and the square of a whole number is another (higher) whole number.
We multiply both members in the fraction times the conjugate of the denominator, which is: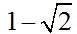 
.
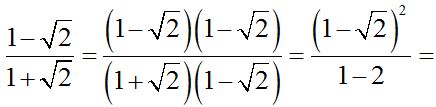
In the numerator, we have the square of the difference of two numbers; which is the same as the square of the first (1) minus 2 times the first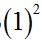 
times the second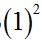
times the square of the second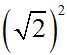 
:
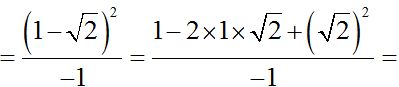
Finally, we multiply times -1 eliminating the denominator,
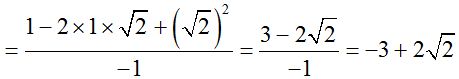
10.85 Calculate:
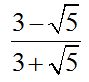Answer: 
.
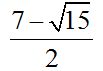Solution:
.
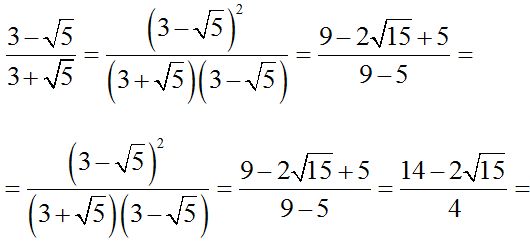
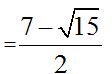10.86 Calculate:
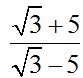. Answer: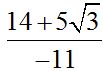 
and also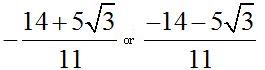 
.
10.87 Calculate:
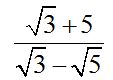Answer: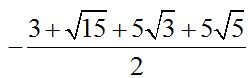 
Solution:
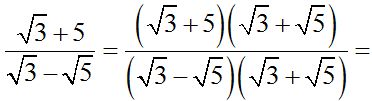
We multiply each term in the multiplier by the terms in the multiplicand. Remember that to be able to multiply square roots, they must have the same index. Then, we multiply the sub-radical quantities: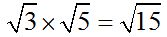 
keeping the same root.
To multiply a number times a square root;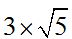 
consider that: 
.
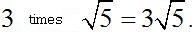Solving the exercise:
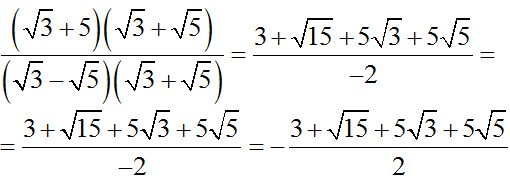
10.88 Calculate:
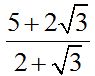Answer: 
.
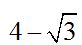Solution:
Solving the exercise step-by-step:
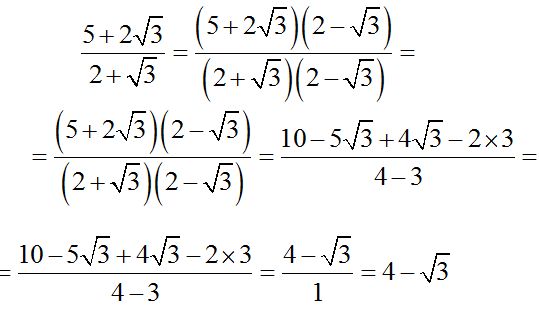
10.89 Calculate:
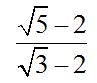Answer: 
.
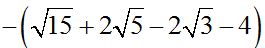