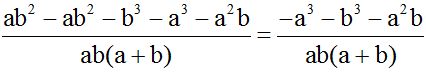Operations with Algebraic Fractions.
10.9 Calculate:
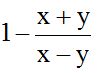Answer: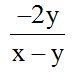 
Solution:
Same as the previous exercise. except that instead of adding, we will subtract. You must be careful with the negative sign in front of a fraction. A negative sign in front of a fraction only affects the numerator. When adding or subtracting other values, each term changes sign:
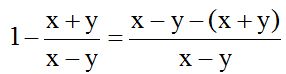
The least common denominator (LCD) will be (x – y). We multiply it by 1 getting x – y. Then, we write the negative sign. We place the second numerator inside parenthesis and we multiply it times 1 because (x – y) divided by (x – y) equals 1.
Now, I remove the parenthesis from the numerator:
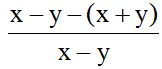
Remember that whenever there is a negative sign in front of a parenthesis, when we remove it, each term inside the parenthesis changes to the opposite sign:
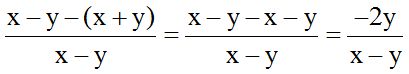
10.10 Calculate:
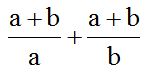Answer: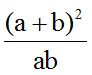 
Solution:
The LCD will be ‘ab’.
We multiply the first numerator times ‘b’ because
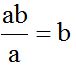
We multiply the second numerator times ‘a’ because
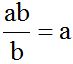
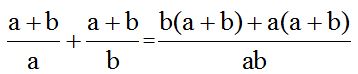
We remove the parenthesis by multiplying the value outside the parenthesis by each one of the values found inside the parenthesis:
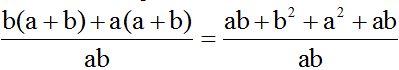
We simplify similar terms. Then, we organize the terms:
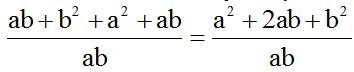
As you can see, the numerator is the square of the sum of two numbers:
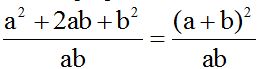
Another solution would come from:
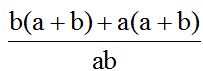
As you can see, there are two terms with the common factor (a + b) in the numerator. I get a common factor for (a + b):
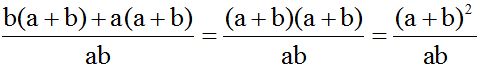
10.11 Calculate:
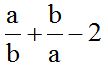Answer: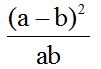 
10.12 Calculate:
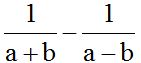Answer: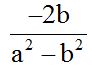 
Solution:
The LCD for both fractions will be (a + b)(a – b).
It is as if you had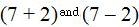 
. The l.c.m.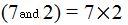 
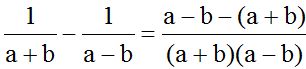
Multiply the numerator of the second fraction -with the negative sign in front- by (a + b). Then, we write the product inside parenthesis. We remove the parenthesis changing the sign of each term found inside the parenthesis. Finally, we reduce (simplify) any similar terms:
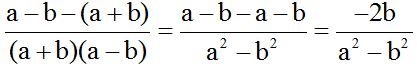
10.13 Calculate:
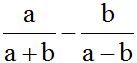Answer: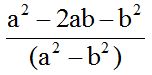 
Solution:
The LCD for both fractions will be the product of both denominators (a + b)(a – b). It is as if you had (5 + 2) and (5 – 2), in other words, 7 and 3. The least common multiple (l.c.m.) is: 7 X 3
We divide (a + b)(a – b) by (a + b):
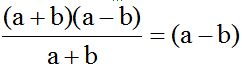
The resulting quotient is multiplied by ‘a’.
We do the same to the second denominator: We divide (a + b)(a – b) by (a – b). The resulting quotient is multiplied by ‘b’:
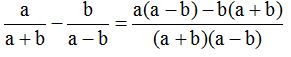
10.14
Calculate the value of:
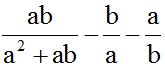Answer: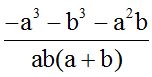 
Solution:
First, we analyse what can be done on each fraction. As you can see, we can simplify the common factor 'a' from the first denominator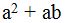 
:
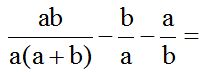
In the first numerator, we have the product ‘ab’ and we have 2 factors in the denominator: ‘a’ and ‘(a+b)’. We can simplify the factor ‘a’ in the numerator with the factor ‘a’ in the denominator. We will get this:
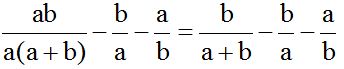
Calculate the l.c.m. of the denominators composed by: (a+b), a, and b. Imagine that a = 7 and b = 3: we would have to calculate the l.c.m. (10, 7 and 3), which would be the product of all 3.
The l.c.m. of (a+b), a, and b is ab(a+b). We divide this value by each denominator and we multiply their quotient times its corresponding numerator :
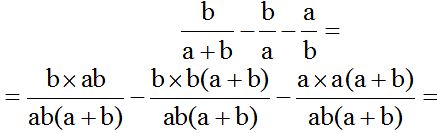
To save time, we will write everything under one fraction because their denominators are equal. Be careful with the alphabetical order and negative signs found in front of parenthesis (when we are removing them):
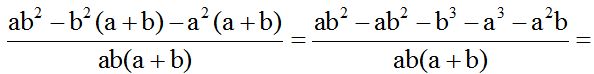
We simplify any similar terms we have:
