Operations with Algebraic Fractions.
10.15 Calculate:
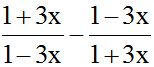Answer: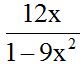 
Solution:
The l.c.m. of the denominators is the product of both: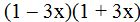 
Divide it by each denominator. Multiply their quotient by their corresponding numerator. This is an example of the first fraction:
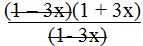
We have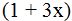 
as quotient. We multiply it by the first numerator, which is also 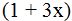. We follow the same process with the second fraction:
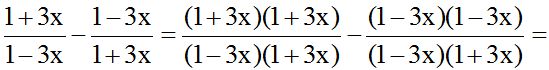
The first numerator is the square of the difference of two numbers and the LCD is equal to a difference of squares:
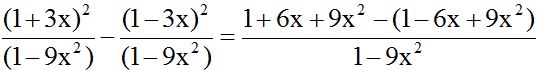
We develop the squares of the difference and the sum of the squares of two numbers.
After the negative sign joining the fractions, we write a parenthesis. When we remove them, we change the sign of each term. Then, we reduce any similar terms:
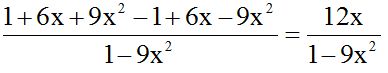
10.16 Calculate:
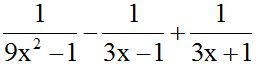Answer: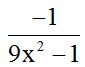 
or: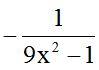 
Solution:
The first denominator is the result of multiplying the sum of two numbers by their difference;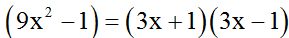 
. Then, the l.c.m. of the denominators will be 
.
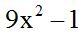We divide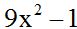 
by the second denominator 
:
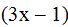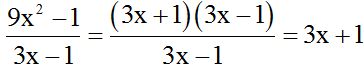
Be careful when you remove a parenthesis with a negative sign in front. We simplify any similar terms:
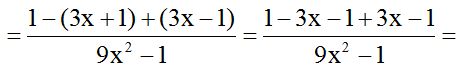
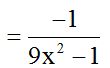
Since a negative sign in front of a fraction only affects the numerator, we could write this result:
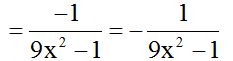
10.17 Calculate:
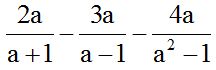Answer: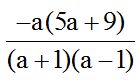 
or: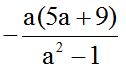 
Solution
Step-by-step:
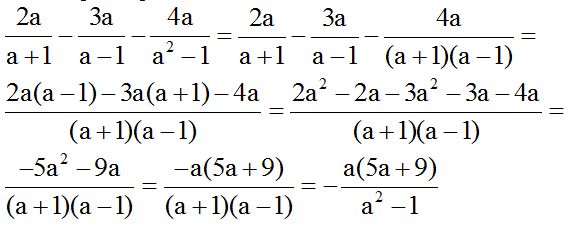
10.18 Calculate:
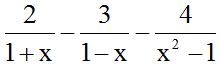Answer: 
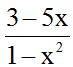or :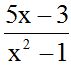 
Solution:
The third denominator: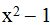 
is not a product of the other two denominators. The second denominator 
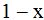won't work; it would have to be 
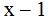. The first denominator 
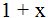works because we can write it as
.
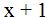We have already mentioned that a negative sign in front of a fraction only affects the numerator and this is important in what you are about to see. If we change the sign to both terms in a fraction (numerator and denominator), the result is the same:
Pay attention to the next example:
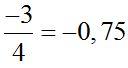
If we change the signs to the numerator and denominator, the result will be the same:
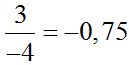
Notice now the same example with the negative sign in front of the fraction:
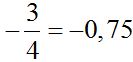
As you can see, the result of all cases is the same.
If we have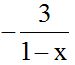
, it would be the same as writing: 
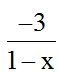because the negative sign in front of a fraction only affects the numerator.
Imagine that instead of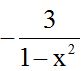 
we want the denominator to be
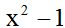: As you can see, we changed the signs of each term in the denominator. If we change the signs of the terms in the denominator, we also have to change the signs in the numerator:
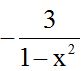
Since the sign in front of a fraction only affects the numerator, we can write:
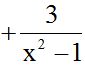
With this in mind, we can solve the exercise:
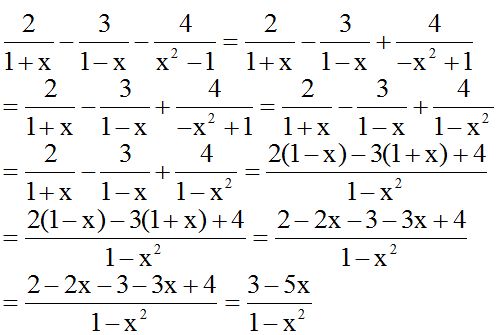
We can also solve it by changing the signs of the numerator and denominator in the second fraction: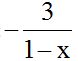 
, which is the same as 
.
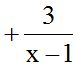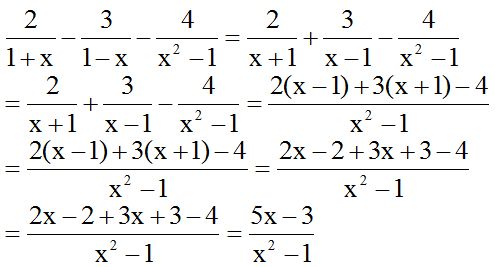
At first look, the results are: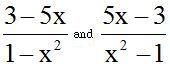 
.
They seem different but in fact they are the same:
Imagine that x = 2. Substitute x with 2 in the first answer:
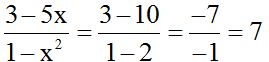
Substitute x with 2 in the second answer:
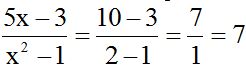
We have the same result in both cases.
If we change the signs of each term in the fraction:
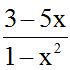the result doesn't vary
.
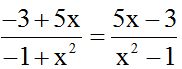10.19 Calculate:
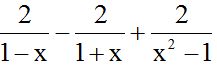Answer: 
.
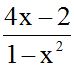Solution:
If the denominator of the third fraction were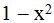 
, it would be the l.c.m. of the denominators. This demands a change in the signs of each term in the numerator and denominator in the exercise:
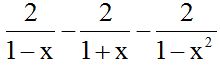
10.20 Calculate:
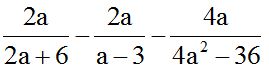
Answer: Any of the three answers is valid:
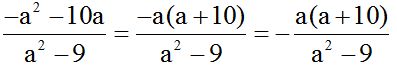
Solution:
We need to analyse each fraction before calculating. In the denominator of the first fraction, we can take 10 as a common factor. In the denominator of the third fraction, we can take 4 as a common factor. In both cases, we can simplify with a factor of its respective numerator:
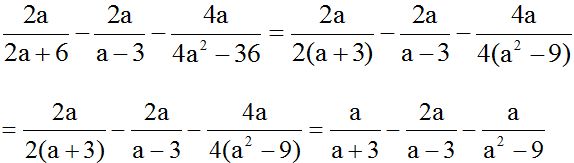
From this, we see that the l.c.m. of the denominators is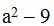 
.
