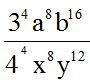Exponents and Radicals of Algebraic Expressions. (Continued)
Imagine we need to solve the following exercise:
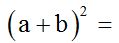
NEVER raise a sum to a power. Whenever terms are adding our subtracting, you need to raise the entire expression to the indicated power. In other words, multiply it by itself the number of times indicated by the exponent.
EXAMPLE:
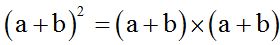
We need to multiply the sum a+b by itself 2 times:
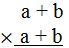
We begin multiplying with the a of the multiplier. Each term in the multiplier is multiplied by each term in the multiplicand. In other words, the a of the multiplier is multiplied by each term in the multiplicand (a+b):
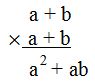
Now, we multiply b by each term in the multiplicand (a+b):
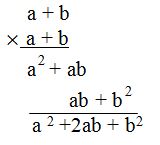
Always keep alphabetical order. Similar terms are placed underneath each other. Remember that terms are similar when they have the same letter variables and the same exponents.
Example: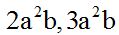 
It doesn't matter if the numerical part of each term is different.
Once we have finished multiplying, we make a line below and add the terms we have calculated:
To raise an algebraic expression to a power, you need to raise each factor to that power. To elevate a power to another, you need to multiply the exponents.
Example: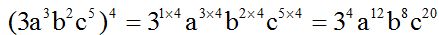 
Both the numerical and literal parts are composed by factors.
10.46 Calculate:
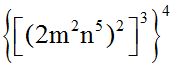Answer: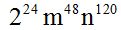 
Solution:
To raise a power to another, we multiply the exponents.
CASE 2.- monomials with negative base:
10.47 Calculate:
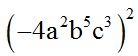Answer: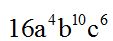 
Solution:
When the base is negative, you need to notice the power to which we need to raise. If the exponent is even, the result will be positive; if the exponent is odd, the result will be negative:
Examples:
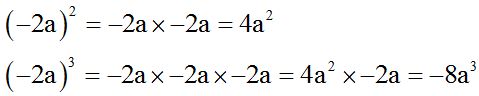
To be able to solve these exercise, you need to know:
1st. These are the rules for multiplying and dividing with signs:
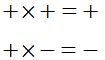and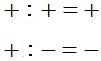 
2nd. To multiply powers with the same base, we add the exponents.
3rd. To raise a power to another, we multiply the exponents.
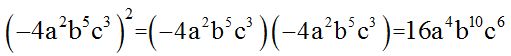
10.48 Are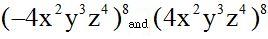 
equal?
Answer: Yes
Solution:
They are equal because any power with a negative or positive base and an even exponent always gives a positive result.
10.49 Calculate:
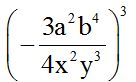Answer: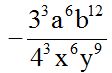 
Solution:
Remember: When the number of negative signs is odd, the result is negative. When the number of negative signs is even, the result is positive.
10.50 Calculate:
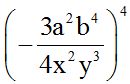Answer: 
