Simplifying Radicals
This is a very simple operation which is useful in many circumstances.
The value of a radical is not affected if you multiply or divide the index and exponent of the radicant by the same number.
10.52 Simplify:
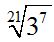Answer: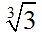 
Solution:
We can divide the index 21 and the exponent 7 by 7. Their quotients will be 3 (new index) and 1 (new exponent for the radicant):
10.53 Simplify:
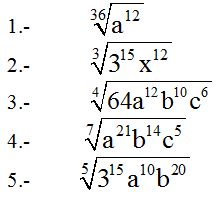
Answers:
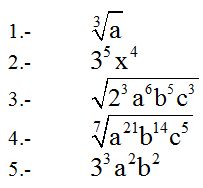
Solutions:
1.- step-by-step, we have: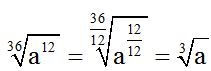 
2.- When the quotient for the index is equal to 1, the radical disappears:
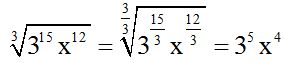
3.- Whenever you simplify the index and exponents inside a radical, we must divide each one by the LCD (least common denominator) of all of them. In this exercise, the number which is able to divide 4, 6,12 and 10 is 2:
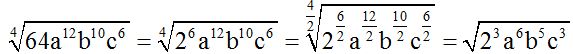
What would happen if there was another factor with an exponent: 1, 3, 5, 7?
Simple, you leave it as it is. Prove this in the following exercise:
4.- 
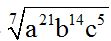
There is no number capable to divide: 7, 21, 14 and 5 an exact number of times (except for 1). If we only had the exponents: 7, 21 and 14, the LCD of all three would be 7. However, since we have 5 as an exponent, there is no answer.
There only needs to be one exponent we can't divide for us not to be able to simplify the radical.
Adding and Subtracting Radicals.
10.54 Calculate: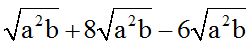 
Answer: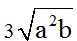 
Solution:
You need to have all indices in all radicals and radicants equal. In this exercise, we have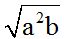 
9 positive times and 6 negative times. It is the same as if we had 9 € - 6 €, in which € = .
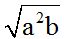10.55 Calculate: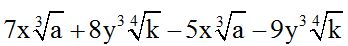 
Answer: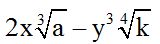 
Solution:
We have gathered similar terms and simplified them separately.
10.56 Calculate:
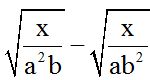Answer: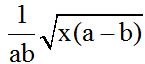 
Solution:
Since both square roots have the same index, we subtract the radicants. The LCD is 
because it encompassed both denominators.
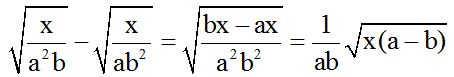
We divide this common denominator by the first denominator and we multiply the 'b' quotient by its numerator.
We divide this common denominator by the second denominator and we multiply the 'a' quotient by its numerator.
Since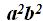 
has an exact square root: 
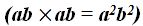, it will be withdrawn from the square root. However, ab will come out as a denominator. We will add 1 as a numerator since we haven't been able to withdraw anything from the numerator inside the radicant.
10.57 Calculate: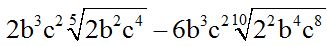 
Answer: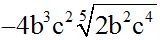 
Solution:
Notice that in the second term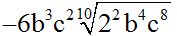 
we can simplify the index and exponents inside the radicant dividing them by 2.
Now, we have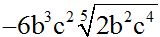 
. Now, both terms are similar. We can subtract them. To do this, we calculate the difference in the numerical part keeping the literal part.
10.58 Calculate: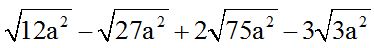 
Answer: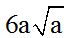 
.
Solution:
We decompose the numerical part of each square root into two factors, one of them keeping the exponent:
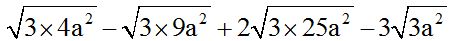
We withdraw the factors with exact squares from the radical and simplify similar terms:
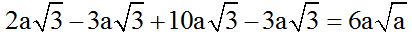
10.59 Find the answer to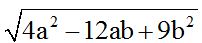 
Answer: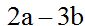 
.
Solution:
We see that the radical has 3 terms inside it. Two of them are perfect squares and the other one has a negative sign. This gives me a hint to know if we are dealing with the square of the difference of two numbers.
We find the square root of the terms with exponents of 2. We write a negative sign between them. We raise this difference to the square knowing that the square root of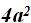 
is 2a and the square root of 
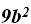is 3b.
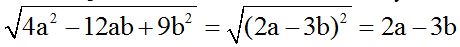
10.60 Do you think this fraction: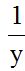 
is equal to this other fraction: 
?
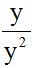Explain your answer whether they are the same or not..
Answer: yes
Solution:
We simply need to remember that if we multiply the numerator and denominator of a fraction by the same number, the value of that fraction doesn't vary:
We multiply the numerator and denominator of this fraction: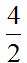
times 3 and we get 
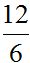. Both fractions have the same exact quotient, which is 2.
The same thing happens with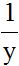 
: if we multiply the numerator and denominator by ‘y’, we get the same fraction: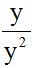
10.61 Are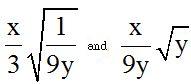 
equal?
Answer: yes
Solution:
If we multiply the numerator and denominator of the fraction inside the radical times ‘y’, we will get:
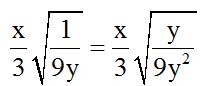
We can see that we can extract 3y from the denominator inside the radical. This leaves a number 1, which is not written:
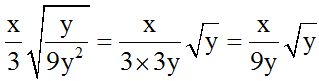
10.62 Can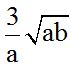 
and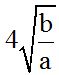 
be added? If so, calculate the result:
Answer: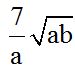 
Solution:
We notice that in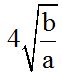 
, we can multiply the numerator and denominator of the fraction inside the radical by the denominator. Then, we withdraw anything we can from the radical:
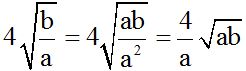
We can see that both addends are similar because their literal parts are equal. This allows us to add their coefficients:
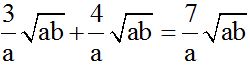
The Radical of a Radical.
It means finding the radical of another radical. This is very similar to raising a power to another. As you probably remember, we need to multiply the exponents:
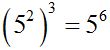
In the case of radicals, we multiply the indices keeping the same sub-radical quantity:
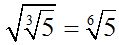
We will reach the same answer if we consider this exercise in exponents:
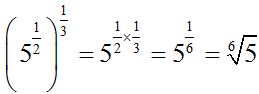
Remember that to write a radical in the form of a power: we write the radicant raised to a power whose numerator is the exponent of the radicant (in the example, 5 has an exponent of 1) and we write the index of the radical as a denominator. From here, we work on it as if we were raising one power to another. We will get to the same result.
10.63 Calculate:
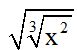Answer: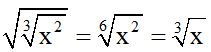 
Solution
Don't forget to simplify the square root dividing the index and exponents of the radicant by the same number:
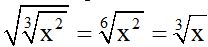
10.64 Calculate: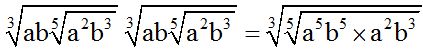 
Answer: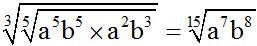 
Solution:
First, we introduce the radicant in the cube root into the radical with index 5: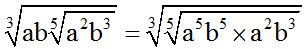 
.
Remember that to introduce factor into a radicant we multiply the exponents of each factor outside the radical by the index. Since they have the same bases once they are inside, we add the exponents:
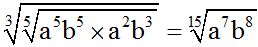
10.65 Calculate: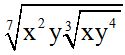 
Answer: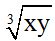 
.
Solution:
Here you have it solved step-by-step:
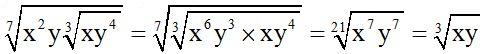
10.66 Find the value of:
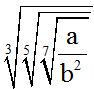Answer: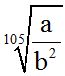 
10.67 Find the value of: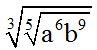 
Answer: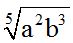 
.
