AREAS OF GEOMETRIC SHAPES
We previously studied the areas of plane geometric shapes (volumes). In this course, we will study the surfaces composed by geometric shapes or solid shapes.
We understand that at solid shape equals a shape that occupies an area (place) in space. In other words, a shape has three dimensions (length, width and height).
If this solid shape has the form of a polyhedron, prism, or round shape, we can refer to them as geometric shapes.
AREAS OF REGULAR POLYHEDRONS
If you recall, we studied the volumes of 5 regular polyhedrons. Now, we will study how to calculate their surfaces.
Regular polyhedrons have equal sides (all its sides).
1) tetrahedron.- Its four sides are equilateral triangles.
We will find the total area of this geometric shape by calculating the area of one side and multiplying it times 4.
For this, we need to know the apothem (or the height of one side of the polyhedron). .
We will calculate the height of one side from the following shape:
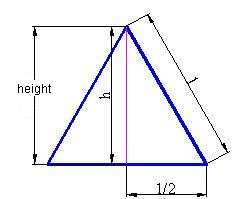
We give a value of 1 to the edge or triangle side to ease our calculation and not have to learn any formulas.
In each case, we apply basic geometry knowledge with a little common sense.
First, we calculate the height, which we will represent as h.
The hypotenuse has a value of 1 and a cathetus - also called leg - (half the base, which measures 1/2). Using the Pythagorean theorem, we get:
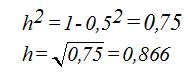
The area of one face when the edge equals 1 will be:
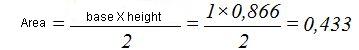
When the side of a triangle or edge of a face equals a, the area will be:
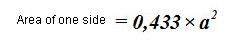
We elevate the edge to a power of two (square) to consider it in two dimensions:
length and width 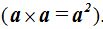
Since a tetrahedron has 4 faces, the total surface will be: 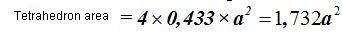
15(4).1 Find the total surface of a tetrahedron with an edge of 5 cm.
Answer: 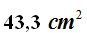
2) Octahedron.- Its 8 equal faces are equilateral triangles.
Each equilateral triangle of a tetrahedron with a side equal to 1 has a surface of 0,433, as we have seen.
Since an octahedron has 8 faces, we will multiply the previous surface by 8 times the value of the square of the side of the triangle or the edge of such octahedron:
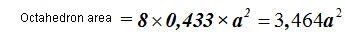
15(4).2 Calculate the total area of an octahedron with an edge of 5 cm.
Answer: 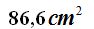
3) icosahedron.- Its 20 equal faces are equilateral triangles.
Because each face has a surface of 0,433, and the side has a value of 1, the total surface of this shape will be:
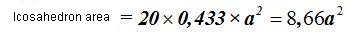
15(4).3 Calculate the total area of an icosahedron with an edge of 5 cm.
Answer: 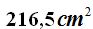
4) Cube.- Its 6 faces are equal squares. The area of each face will be the value of that face times itself, in other words:

The total area of the cube will be, we will call the value of 1 face of a square (or edge of a cube) a:
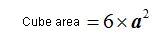
15(4).4 Calculate the total area of a cube with an edge of 5 cm.
Answer: 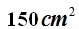
5) Dodecahedron.- A dodecahedron is composed by 12 equal pentagons. When we studied 15(3) (previous course), we deducted that the area of one of them (with a side a or edge of a dodecahedron) is:
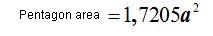
To know the total area of a dodecahedron, we will multiply the area of one face by 12:
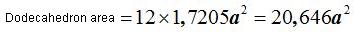
15(4).5 Calculate the total area of a dodecahedron with an edge of 5 cm.
Answer: