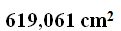AREAS OF REGULAR PRISMS (Continued)
The development of a regular prism whose base is a pentagon is:
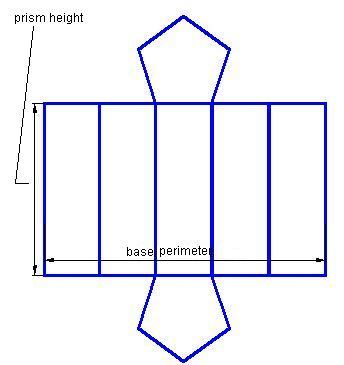
The side area equals to the base perimeter (the sum of the measurements of the 5 sides of the pentagon) times the height of the prism or edge side.
We will call the perimeter P, we will call the height h
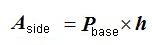
The total area equals the side area plus the area of the two bases, which are 2 equal pentagons.
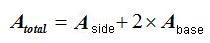
A problem emerges in a pentagon when we have to calculate the area of an isosceles triangle, as we divide it in 5, just like we studied in 15(3) when we calculated the volume of the dodecahedron.
Using 1 as the length of one side of the pentagon and using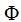 
; each one of the equal sides in an isosceles triangle equals 0,8506, in which the height equals:
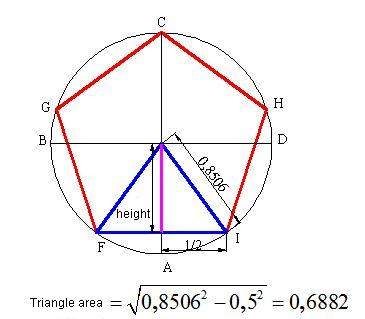
The area of a triangle will be:
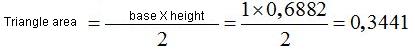
And the area of the 5 triangles will be:
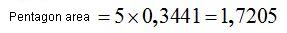
This result will work with a side measuring 1; if we are talking of a new value, a, we will multiply it times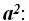 
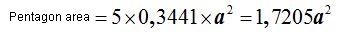
The total area, using a as the side of the pentagon and h as the height of the prism, will be:
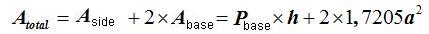
15(4).9 What is the total surface of a prism with a pentagon base of 3 cm. per side and a height of 10 cm?
Answer: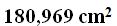 
Solution
Substitute these values into the formula:
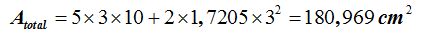
The development of a regular prism whose base is a hexagon is:
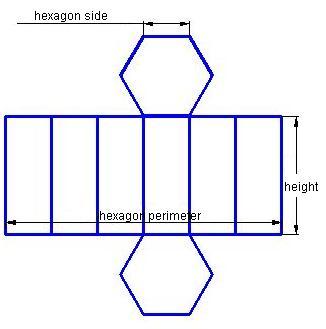
The side area equals the base perimeter (the sum of the measurements of the 6 sides of the hexagon) times the height of the prism or edge side.
We will call the perimeter P, we will call the height h
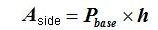
The total area equals the side area plus the area of the two bases, which are 2 equal hexagons, will be:
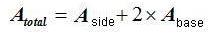
15(4).10 What is the total surface of a prism with a hexagon base of 3 cm. per side and a height of 10 cm?
Answer: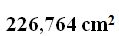 
Solution
We calculate the side area:
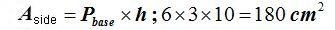
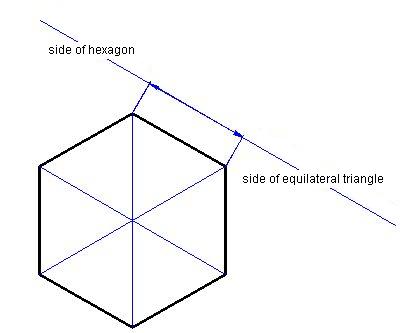
A hexagon has 6 equilateral triangles:
We calculate the height of a triangle :
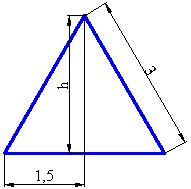
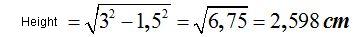
The area of the base will be 6 times the base of a triangle:
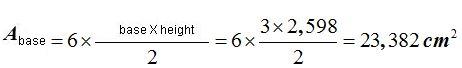
The total area will be:
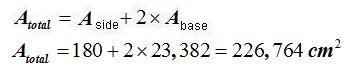
15(4).11 What is the total surface of a prism with a hexagon base of 6 cm. per side and a height of 12 cm?
Answer: 
