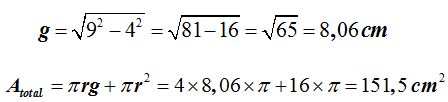THE CONE
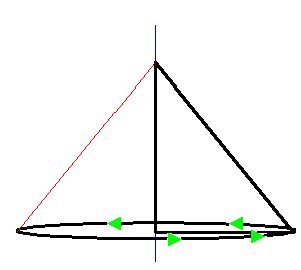
A right triangle spinning around on one of its legs generates, produces, or creates a cone:
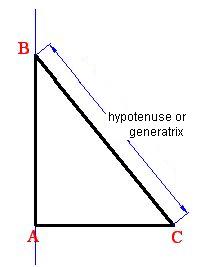
On the right triangle in the image above, leg AB works as a rotation axis.
As the triangle spins around axis AB, the hypotenuse or generatrix will create the cone:
To create a cone, you need a circle, which will work as base, and a circular sector found between one generatrix and another (1 and 2, respectively).The curved base equals the length of the base circumference:
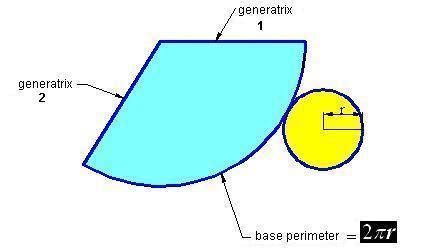
In the image above, you can see the circle corresponding to the base of the cone (in yellow) and the side surface (in blue), which equals the circular sector found between generatrix 1 and generatrix 2, whose curved base equals the length of the circumference of the base circle, in other words,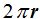 
To calculate the side area, we can consider the circular sector as if it were a triangle with a base of 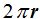and a height equal to the generatrix:
We will call the base perimeter P, and we will call the generatrix g.
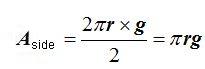
The total area equals the side area plus the area of the base:
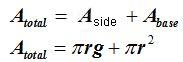
15(4).14 Calculate the side area and the total area of a cone whose generatrix equals 10 cm. and the radius of the base equals 5 cm.
Answers: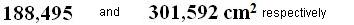 
15(4).15 Calculate the total area of a cone whose measurements are shown in the image below:
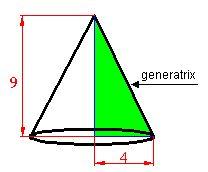
Answers: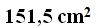 
Solution
We need to know the value of the generatrix or hypotenuse of the right triangle (in green). Since we know the value for each one of its legs, we can get the value of the generatrix (Pythagorean theorem):
