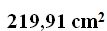SPHERICAL CAP.
We call a spherical cap to any of the two parts left once a sphere has been divided (cut) by a secant plane:
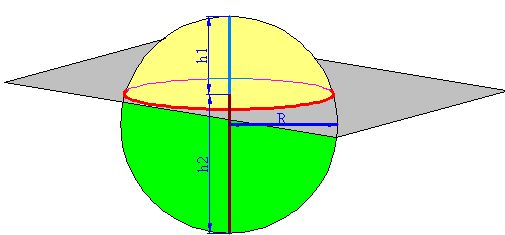
In the image above, we can see both spherical caps (green and yellow), with heights h1 and h2, and a radius of the sphere R.
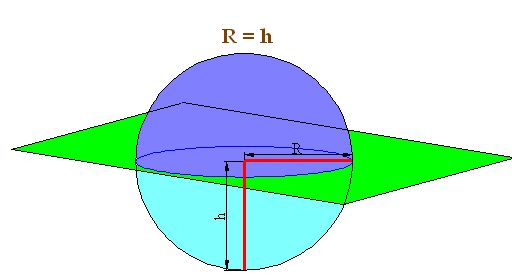
To calculate the area of a spherical cap, we can use what we studied for spherical zones and use the same formula. In the following image, notice that the height (h) and radius (R) are equal.
In this case, we have two equal spherical caps. Each one equals half a sphere:
Remember that we deducted that the area of a sphere equals to:
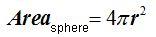
This means that each semi-sphere has a surface of:
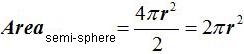
Since we have seen that semi-sphere equals to a spherical cap in which its height and the radius of the sphere are equal, we can write this formula:
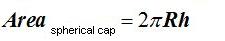
15(4).22 Calculate the area of a spherical cap of 5cm., high. The radius of the sphere equals 7 cm.
Answer: