Free sourse

In F 22, we have two equivalent triangles. Their sides are the same. We need to find the rotation centre. In order to move from one position to another, we have performed a rotation whose centre is a point located outside the shapes.

First, we are going to remember how to calculate the circumcentre of a triangle (valid for any polygonal shape). The circumcentre is the point where the bisectors meet, in this case, a triangle. A bisector of a segment is the perpendicular line of that segment exactly in its middle point. Let's analyse how to find the circumcentre step-by-step:

We trace the bisector for line AB. First, we need to know where its middle point is. We take a compass and, using the same radius and making centre in A, we trace two arches. We do the same with B. The arches traced from both A and B will intersect as seen in F 22:

This way, we have calculated the mid-point of segment AB. Then, we trace a perpendicular line from this point (in green) to determine the first bisector.

We do the same thing from points BC and CA in red and blue to determine the other two bisectors.

Here you have it in F 23:

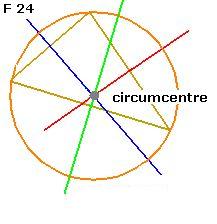
The point where the three bisectors of the triangle meet or cut is called circumcentre.

In F 24, we can see the circumference that surrounds or circumscribes the triangle.

We will determine the rotation centre of two counterpart segments.

In F 25, we have two segments: AB and BB’. Segment A’B’ is the counterpart of AB. We can see that segment A’B’ has rotated around a point outside both segments.

We need to calculate the rotation centre. To do this, we join points A with A’ and B with B’ to calculate their bisectors (F 26):

We can prove that the bisectors of two segments are two perpendicular lines to their own mid-points. These segments are: AA’ and BB’

Using the circumcentre, we trace arches from points A and B until they transform into their equivalent counterparts A’ and B’ (F 27):

	Lesson 10ª