ROTATED ANGLE.
Once we know the rotation centre, we can easily determine the angle in which the shapes have rotated.
In F 28, the values of angles AOA’ and BOB’ are equal; they are both 140º and it is the angle rotated from segment AB to A’B’.
ROTATION CENTRE AND ANGLE OF TWO COUNTERPART TRIANGLES.
The process is the same as we have studied so far.
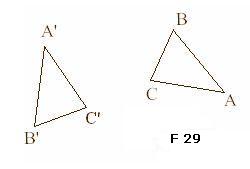
In F 29, we have two equivalent (counterpart) triangles. We will determine the rotation centre and the value of the rotation angle.
In F 30, we have the bisectors of the lines AA’, BB’ and CC’, which define the circumcentre.
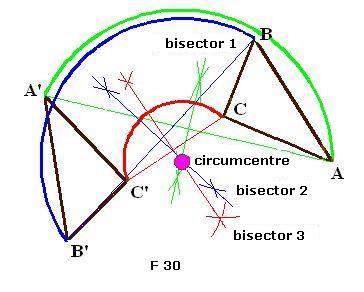
Using this circumcentre, we trace arches in green, red, and blue as described by vertices A, B and C to A’, B’ and C’.
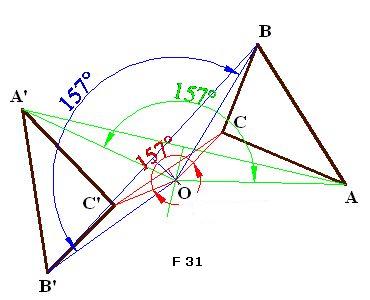
If we take a closer look at F 31, we can see that the angles that form AOA’ (in green), BOB’ (in blue) and COC’ (in red) represent the rotation angle, which logically, have to be the same. In this case, we find that the rotation angle is 157º.
SYMMETRY IN THE PLANE.
When the position of a shape in the plane, its dimensions and form, correspond to one and another side of a point, an axis or a plane, we can say they are symmetrical shapes. Such shapes must be found at an equal distance of the point, axis or plane of symmetry:
In F.1, point O, or the centre of the circumference (circumcentre), is the middle point for every line.
Point O is the centre of symmetry.
If we take any segment, for example, OD and we fold it by the middle (point O), we will find it coincides with OD’.
Point O is found at an equal distance of points A and A’, B and B’, C and C’, and D and D’.
Points AOA’, BOB’, COC’ and DOD’ are aligned.
Instead of using points, as in the previous case, let's analyse the segments that form the pentagons in F.2. In this case, both pentagons are symmetrical is relation to a central point of symmetry; O:
In F. 3, we see that the segments that join the counterpart points AA’, BB’, CC’, DD’ and EE’ go through point O, which is the symmetry point:
If we fold a sheet of paper with the contents of F.3 through point O con with its corresponding inclination, both pentagons would coincide.