AXIAL SYMMETRY.
The word 'axial' comes from the latin “axis” and axial symmetry means symmetry in relation to an axis. For example, in F.4(a), we have point A and its equivalent A’. If we fold a sheet of paper with this shape through the axis of symmetry, points A and A’ will coincide:
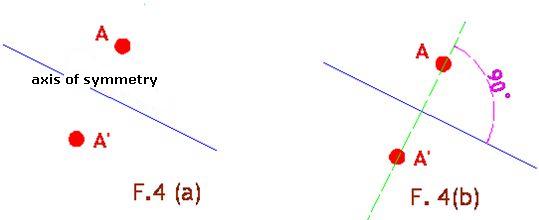
The line (in green) going through points A and A’ is perpendicular to the axis of symmetry and both points are found at equal distances from the axis. Let's apply the axis of symmetry to a triangle:
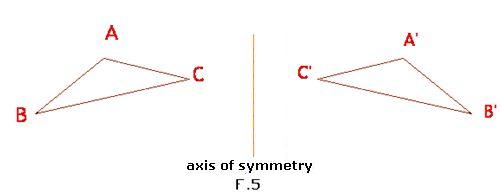
You can test if both shapes are located at equal distances from the axis of symmetry. If we folded a sheet of paper with F.5 in it through the axis of symmetry, both shapes would coincide. coincide.
We apply the axis of symmetry to create a shape which includes several lines as you see in F.6(a)
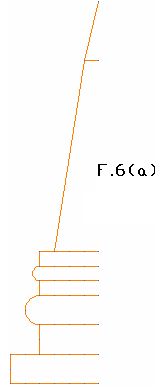
First, we draw one half of the shape; you don't need to draw it complete.
Then, we trace the axis of symmetry just as you see in F.6 (b) with its reflection symmetry of F.6(a).
As you can see, the distance of both halves to the axis of symmetry is the same.
If we eliminate the distance between both counterpart shapes, we will get the complete shape F.6 (c)
Homothety is the geometrical transformation which affects a shape. Starting from a point, all measurements are multiplied by the same factor (different from zero).
In F.7, we have some coordinates (points). Triangle ABC has its corners (vertices) in points A(– 2,3), B(4,2) and C(1,2).
We multiply the coordinates of each point time the factor 2. These values will transform into: A’(– 4,6), B’(8,4) and C’(2,4).
The homothetic centre has been placed in O, which corresponds to (0,0) in the coordinate axis.
In F.8, the values of the points of the vertices of triangle ABC are A(3,0), B(4,1) and C(2,4).
The factor is 2, thus, the vertices of triangle A’B’C’ will be: (6,0), (8,2) and (4,8) respectively.
When we join the vertices of homothetic shapes with lines, these come together in a point called the homothetic centre (in previous and future examples, they will be represented by the letter O).
In Homothety, we need to bear in mind the original shape and the homothetic shape. Both will have the same form but their size will be different depending if the factor or scale factor (generally represented with the consonant k - k factor, but the consonant c is also used) is greater or lower than one unit.
In F.9, we see that there hasn't been a modification in size since we are dealing with a point (A), but we have a modification in distance:
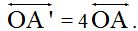
In this example, A’ is the counterpart of A.
If the k factor is lower than the unit (1), as in F.10, point A’ will be located between the origin O and point A.
Distance OA’ will equal to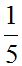 
of distance OA:
: 
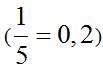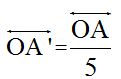
The same thing happens in homothetic shapes when k is lower than a unit.
In F. 11, we see that triangle A’B’C’ is located between the homothetic centre O and triangle ABC.
What happens when k<0?
In this case, we mean that the value of the factor is negative. Take a look at F.12.
We have a coordinate axis. The coordinates of point A are (1,7), B(2,5) and C(– 2,3).
The scale factor or k = – 2.
The coordinates of A’ are (4, –6), B’(–4, –10) and C’(–4, –14).
When we join AA’, BB’ and CC’ with dotted lines (in red) going through the homothetic centre O, we produce a larger and inverse shape.
Triangle A’B’C’ is larger and inverse in relation to triangle ABC.
