ADDING SEVERAL VECTORS:
If we need to add several vectors, first we add two to find their resulting value. Then, we take this resulting vector and add it to the next vector. We add this new resulting vector to another vector, and so on and so forth until we have added all the vectors we need to add.
OPPOSITE VECTOR.
An opposite vector (also called additive inverse) of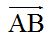 
has the same magnitude and direction but an opposite sense:
The opposite vector of 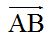would be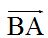 
In a graphic: Vector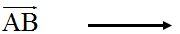 
opposite vector 
If the coordinates of vector 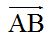were (5,7), those of vector 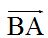would be (– 5 , – 7), which we can write as: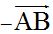 
and also: – (5,7)
Remember that if you remove the parenthesis whenever there is a negative sign in front of it, the terms found inside will change their signs: – 5 , – 7.
Here we have vector 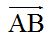and its opposite vector :
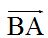POSITION VECTOR.
A position vector is that vector whose initial point is found in the origin of the coordinate axis. In other words, it is found at point (0,0). When adding or subtracting vectors, it is easier to place the initial points of vectors at the origin of the coordinate axis.
8.14 What is the result of adding two opposite vectors?
Answer: zero.
Solution:
Since they have the same magnitude but opposite senses, their sum would be zero. If their magnitude equals 3, the sum with their opposite, which is – 3, will give us a result of: 3 – 3 = 0
SUBTRACTING VECTORS.
If we want to subtract two vectors: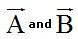
, we add the first to the opposite of the second. Try to follow this procedure step-by-step:
Both vectors have the same initial point: (0,0). Vector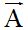 
has a terminal point at (1,5). Vector
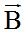has a terminal point at (5,4). First, we will solve this by subtracting their components:
We subtract the components of 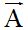and those of :
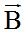(1 – 5, 5 – 4) =(– 4 , 1)
As you can see in F 8, this coincides with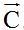 
. Graphically, after placing the two vectors to be subtracted, we need to place the opposite of the negative vector. In this case, we need to place the opposite of vector 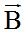(same magnitude but opposite senses). We have drawn this in red. Trace the parallels of vectors 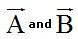bearing in mind that we are referring to the opposite of vector 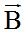. We join the intersection of both parallels with the initial points of 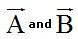, in other words, (0,0) and we get the vector with coordinates corresponding to (– 4, 1).
8.15 We have two vectors; vector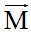 
, whose initial point is (0,0) and terminal point is (1,5), and vector 
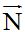, whose initial point is (0,0) and terminal point is (6,1). Find their difference graphically.
Answer: initial point (0,0), terminal point (–5,4)
Solution:
We need to subtract vector 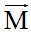from vector 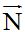. Here you have them in F 9.
We trace the opposite of vector 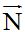(in red) with vector 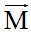. For this sum, as always, we trace the parallels of vector 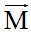and the opposite of vector 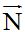. We join the point where these two parallel lines cut or meet with the initial point of both vectors (0,0). We will get the value of the subtraction. As you can see, the components are (0,0) at its initial point and (– 5, 4) at the terminal point.
To prove this, add the components of the first segment with the opposite of the second: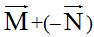 
= (1– 6, 5 – 1) = (–5,4).
8.16 Vector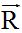 
has an initial point at (0,0) and a terminal point at (5,6). Vector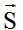 
has an initial point at (0,0) and a terminal point at (6,– 1). Find their difference graphically.
Answer:
coordinates: initial point (0,0) and terminal point (–1, 7)
