MAGNITUDE OF A VECTOR OR SCALARS.
First of all, it is important to properly understand the concept of magnitude. Magnitude is the same as size, dimension, volume, measurement, etc. Any body that can be measured or weighted has a magnitude or measurement or capacity or weight, etc. We can weight or calculate the volume of a rock, for example.
The result of that weight is written with a number followed by its corresponding unit; for example, 5 Kg. If we calculated its volume, it could be 2 dm3
Every magnitudes or measurement we make, which we are able to describe in terms of numbers and units ( 12 Kg, 4m3 , 4 Hl, 3 mm , etc.), are called scalars.
There are other magnitudes, which besides writing a number and type of unit, need more information: quantity, direction and sense. Those magnitudes which need a quantity, direction and sense are called vectorial magnitudes.
When we are talking about a car running at a velocity of 120 Km/hr in the direction of Ávila – Salamanca (Salamanca sense), besides a number of kilometres per hour we indicate its direction and sense. This magnitude will be vectorial.
FIXED VECTORS (BOUND VECTORS)
A fixed vector of any segment, part or portion of a line which is oriented is represented by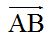 
.
Fixed vectors need to have:
- Initial and terminal point of the segment.
- direction, which is the line upon which the vector is located.
- sense, if its going to the left or to the right, up or down (there are only two possible senses in a vector).
- magnitude, which is the size of the segment.
EQUIPOTENT OR EQUIVALENT VECTORS:
Those vectors which have the same magnitude, direction and sense are called equipotent or equivalent (the have the same value).
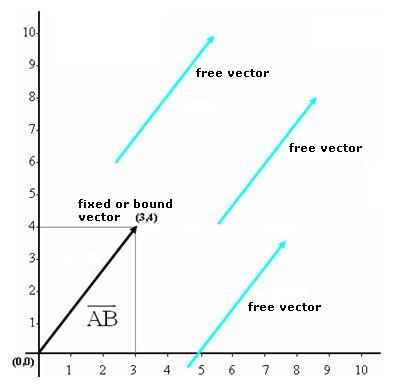
FREE VECTOR
Free vectors are those vectors which have the same magnitude, direction and sense and they can have different initial points and terminal points. In the following image, we have a fixed vector with an initial point at (0,0) and a terminal point at (3,4) and three free equipotent vectors with different initial and terminal points but the same magnitude, direction and sense:
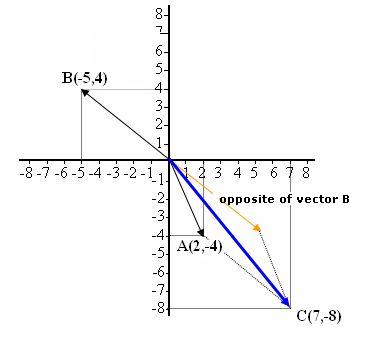
8.17 Find the difference of vectors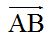graphically. Vector A has>an initial point at (0,0) and a terminal point at (2, –4) and vector B has an initial point at (0,0) and a terminal point at (–5, 4).
Answer: Vector C(7, –8)
Solution:
By the method of subtracting the components, we have:
(2 –(–5), –4 –(4)) = (2+5, –4–4) = (7, –8)
Here you have the solution in the image below. The vector in orange is the opposite of vector B and the vector in blue is vector C, which is the result of the subtraction.
