SUCCESSIVE TRANSLATIONS.

In F I, we have a triangle whose coordinates correspond to points (–2, –1),  (–3, –3) and (–1, –2).

We will perform a translation using the sum of vectorsas guide vectors:

Vector has components (2,4) and vector , (4,4). We calculate the sum of these vectors:

                                     
The components of  are: (2+4,4+4) = (6,8)

You can see this graphically in F II.

The guide vector is represented in blue: 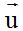 = (6,8).

To calculate the equivalent counterpart points of the triangle vertices, we add the components of each point with the guide vector:

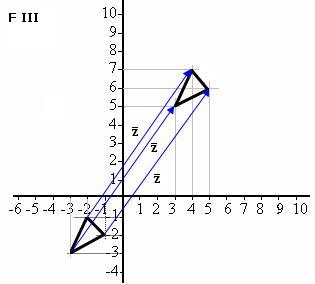
(–2, –1) + (6,8) = (4,7)

(–3, –3) + (6,8) = (3,5)

(–1, –2) + (6,8) = (5,6).

Here you have them graphically in F III.

8.19 Even if it seems like its a lot of work, it is convenient for you to perform the translation of a simple shape considering that the guide vector is the sum of the other two vectors. The values of all the components are your choice.

ROTATIONS IN THE PLANE.

Rotation means turning around an axis or a point. It also means moving an object in a circular manner. Rotations can be done in two senses; to the right or to the left.

When we move an object in a circular manner in a point, we describe an angle. If we rotate it counter-clock wise, the angle will be positive. If we rotate it clock wise, the angle will be negative.

In F 1, we have two rotations: 90º and 180º. Both are positive because the arrows indicate that the rotation has been done in a counter-clock wise sense.

In F 2, we have three angles: 37º, 90º and 143º. They are positive because they are turning in a counter-clock wise sense.

The mid-point of the coordinate axis corresponds to an angle of 180º (F 3).

When an angle goes over 180º, we enter the third quadrant

(F 4):

REMEMBER THE IDEA OF AN ARCH:
An arch is a part, a piece, a portion of a curve. In F 5, you can see the drawing of an apple tied to a string forming a circumference:

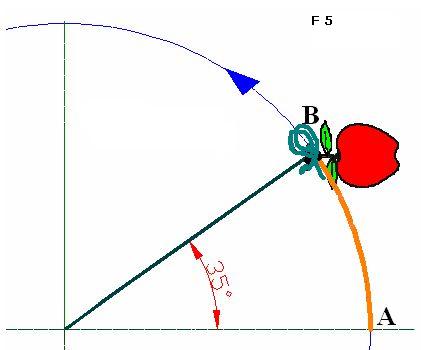
This portion of curve AB represents an arch and it is the path traveled by the apple. A complete turn will be equivalent to the length of the circumference. The arch AB in F 5 corresponds to an angle of 35º. A complete turn corresponds to an angle of 360º.

ROTATION CENTRE:
a) The rotation centre is found inside the shape which is rotating. In F 6, the rotation centre is represented by a red dot. As you can see, this red dot is a part of the shape.

In F 7, we have the result of repeating the shape 6 times in rotations of 60º each, in a positive sense.

INTERESTING EFFECTS:
Through rotations, we can get interesting results when the centre corresponds to the same shape.

As you probably remember, the point where the three heights of a triangle meet or cut is called orthocentre.

In F 8, we have an equilateral triangle (same sides) on a coordinate axis. We will trace the three heights of this triangle bearing in mind that a height is a perpendicular line that joins the vertex with the opposite side.

In F 9, the three heights cut or meet in a point called orthocentre. We place the orthocentre over the origin of the coordinate axis.

In F 10, we draw 4 triangles rotating at 90º using the orthocentre. We have numbered these triangles. We have turned triangle 2 in an angle of 90º in relation to triangle 1. We have done the same with triangles 3, and 4 respectively. Each triangle has a different colour for you to see this clearly.

When we have a greater number of triangles or other shapes, we get interesting results, as you can see in F 11. These are 30 equilateral triangles which have been rotated at 12º one after the other:

ROTATIONS IN THE PLANE WHEN THE ROTATION CENTRE IS NOT A PART OF THE SHAPE:
Let's consider the case in which the rotation centre is found outside the shape (F 12).

In this case, we have performed 10 rotations at 36º, each one with a centre at point (0,0) of the coordinate axis and not from a point inside the shape. We have the distance from each shape to the centre (origin of coordinate axis) in red.

EFFECT OF REPEATING ROTATIONS WITH CENTRES FOUND INSIDE OR OUTSIDE SHAPES:
In F 13, we see that the base of the shape is resting on the origin of the coordinate axis.

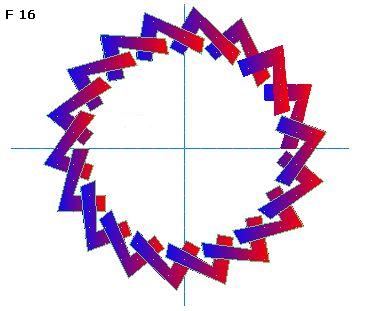
Taking the centre of the base of the shape as a rotation centre, we place 18 repeated shapes, each one at 20º. Notice the result in F 14.

If we relocate this shape away from the origin of the coordinate axis, as seen in F 15, and we place 18 repeated shapes, each one at 20º, we will get a different result (F 16).

Previous Lesson		Next Lesson