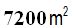AREAS - GEOMETRY.
CONCEPT OF AREA
It would be convenient for you to study this course in a different manner than the usual.
Try not to recite a formula. Instead, try to understand and know what you are saying from the start. This implies a minor supplementary effort which I consider to be very important.
Up to now, we have studied points, lines, angles, polygons, etc. in geometry. We have represented them over a plane. Most of all, we have worked with lines; some curved and some straight, but lines nonetheless. In many exercises, we have only worked on calculating lengths.
From this point on, when studying areas, besides the length, we will need to know another dimension: width or height . Moreover, you need to study this topic using a ruler, a pen, some scissors and paper.
15(2).1 On a sheet of paper, draw a square measuring 1 cm. on its sides. Now, add 9 equal squares, as you can see in the image below. Cut it and now you have a piece of paper 10 cm. long by 1 cm. wide in your hands:
How many 1 cm. squares do you have?
Answer: 10 squares measuring 1 cm. on each side.
15(2).2 Draw a line 10 cm. long and another line 5 cm. wide. Cut it. How many 1 cm. squares do you have?
Answer: 50 squares measuring 1 cm. on each side.
Solution:
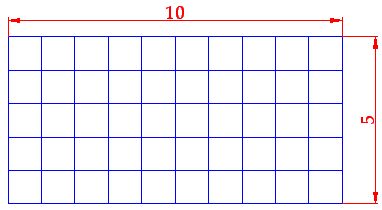
15(2).3 Which is the easiest way of knowing the quantity of 1 cm. squares for the previous image?
Answer: Multiplying the number of squares we have length-wise (10) by the number of squares we have side-wise (5):
15(2).4 You have cut a piece of paper that measures 10 cm. long by 5 cm. wide. If you want to have a piece of paper measuring 8 cm. long by 10 cm. wide, is it necessary to draw 80 squares measuring 1 cm. on each side?
Answer: No, you simply need to draw a line 8 cm. long and another line 10 cm. wide.
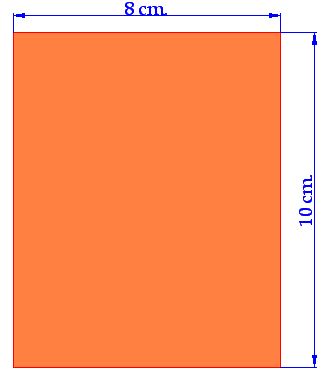
15(2).5 Is this piece of paper measuring 8 cm. long by 10 cm. wide the same as the following image?
Answer:
CALCULATING THE AREA OF A RECTANGLE
When solving an exercise, whenever possible, you must write the answer with the type of unit used in the exercise. For example: 8 Km, 12 Ha, 4 m2., 12 cm., etc
On the previous image, you have a rectangle measuring 8 cm. long by 10 cm. wide. How many square centimetres do you have?
According to what we've been studying, we have: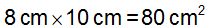 
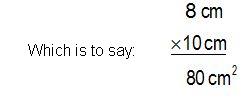
Remember, when multiplying powers with the same base, we must add their exponents; cm has an exponent of 1, so: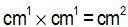 
is the same as:
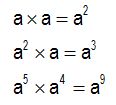
15(2).6 In the following figure, How many square centimetres do we have?
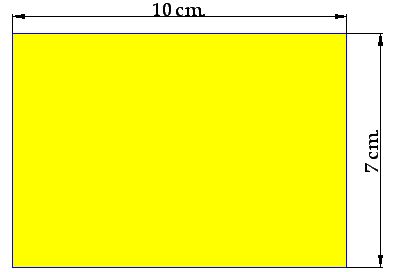
Answer: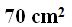 
Solution:
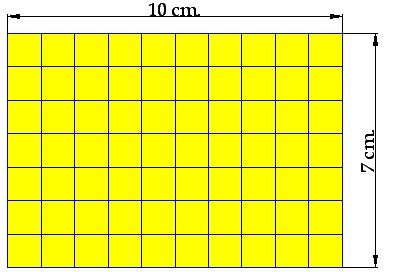
The number of square centimetres is 70 if you count them.
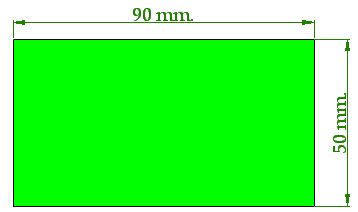
15(2).7 Using a ruler, draw a rectangle measuring 90 millimetres long and 50 millimetres wide. Cut it and test the answer. How many square millimetres does the rectangle have?
Answer: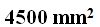 
and the shape is:
15(2).8 How many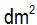 
can you find on a rectangle measuring 4 dm. wide by 3 dm. long?
Answer: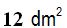 
AREA AND SURFACE
These are words we will use indifferently; they will be the same. Some say the area is the numerical expression obtained after measuring a surface, others say similar things; we will use them indifferently.
All the pieces of paper you have cut have different sizes. As you have seen, to know the exact area of a surface, we need to know two measurement: length and width (or height; imagine a wall measuring 3 metres long and has a height of 5 metres).
15(2).9 What is the area of a rectangular plaza measuring 90 metres long by 80 metres wide?
Answer: 
