GOLDEN OR AUREUS RECTANGLE
A golden rectangle is a rectangle in which the quotient from the value of the longer side divided by the value of the smaller side is the golden number or golden quotient or ratio.
In this moment, you might be thinking, "I didn't understand that".
After performing the following 12 steps, you will have understood half of it.
Let's see:
1) Take a piece of paper, a pen, a ruler and a drafting compass.
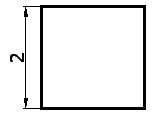
2) Draw a square which measures 2 cm. on each side:
3) Find the middle point for the base (the red dot in the image):
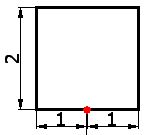
Each half of the base measures 1 cm.
4) Take the ruler and join the above-mentioned middle point with the upper right-hand vertex
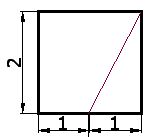
5) Take the compass and draw a circumference using the middle point of the base as centre (red dot in figure on step 3) and a radius equal to the length of the line you drew on step 4:
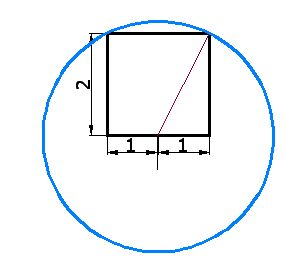
6) Complete the line at the base until it reaches the circumference (as shown in the image below) and erase the rest of the circumference. It should look like this:
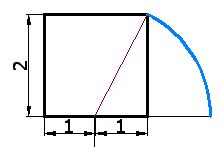
7) Calculate the length of the radius of the circumference, in other words, r:
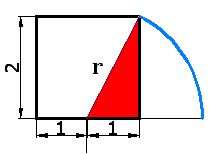
The triangle (in red) is a right-angled triangle in which its catheti (or legs) measure 1 cm. and 2 cm. respectively; the value of r will be equal to the hypotenuse.
We will use the Pythagoras theorem:
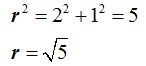
8) The yellow line in the following image will measure:
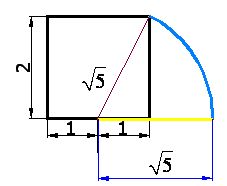
Since it is the radius (hypotenuse of previous image).
9) What is the value of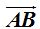
in the following image?
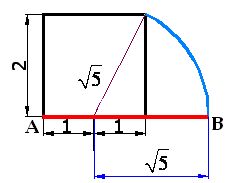
The red line measures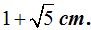 
10) Draw a line of 2 cm. perpendicular to 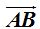starting from point B:
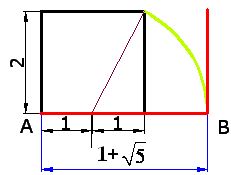
The complete base (in red) now measures: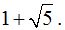 
11) Join the upper right-hand vertex with the perpendicular from point B from the base and write the measurements of the new rectangle:
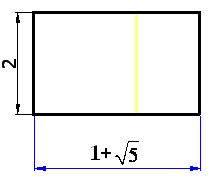
12) Remember we call ratio to the indicated quotient of two numbers.
If we divide the value of the longer side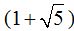 
by the the value of the shorter side (2), which is to say:
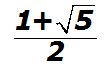
This indicated quotient or ratio is called golden ratio, and the value resulting from this quotient is called golden number or aureus number. It is represented by the Greek letter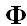 
(Phi) and it has a value of :
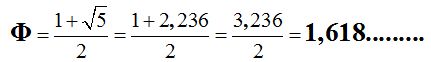
You might say you understood. However, you might be asking yourself: what is the use of this? What for? What is the purpose of knowing this?
The Greeks, several centuries before Christ, stated that this rectangle reflected harmony and extraordinary beauty. Thus, they used these proportions in their most famous monuments (The Parthenon: if you can find a picture, measure its width and height and you will find the golden number). The ancient Egyptians also used the golden ratio (Keops pyramid).
Several centuries later, one of the most brilliant minds in the history of mankind, Leonardo da Vinci (1452 / 1519), deepened the studies and applications for 
(human body- anatomy perfection, Mona Lisa, etc.). Leonardo was responsible for naming them golden ratio, golden number, etc.
Exercise:
Your drivers licence or ID card, does it have a golden rectangle shape? Find out.
For the Greeks, a golden rectangle was both beautiful (for its proportions) and mysterious. There are several pieces of work, studies on some geometrical shapes based on this rectangle, in which you may discover very interesting things (if you like to investigate). It is worth the while.
Golden Spiral:
Using a golden rectangle like the one we have of the following image:
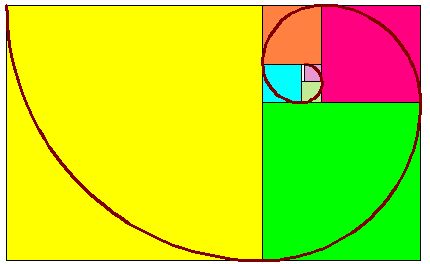
From this golden rectangle, we calculate the yellow square. Using this square, we trace the arch of a circumference using the upper right-hand vertex as a centre, starting our trace from the upper left-hand angle and ending at the lower right-hand vertex (of the same yellow square).
The rest of the shape, in other words, the rest of the image if we remove the yellow square, is another golden rectangle. From this golden rectangle, we calculate the green square. Using this square, we trace the arch of a circumference using the upper left-hand angle as a centre, starting our trace from the lower left-hand vertex and ending at the upper right-hand vertex of the green square.
If we remove both the yellow and green squares from the shape, we will find another golden rectangle. After calculating a new square (red in the image), we repeat the same actions.
Finally, we will get a golden spiral, which has applications in arts, architecture, sculpture, etc. for both its harmony and beauty. We can also find golden spirals in sea shells for some mollusks. It is interesting to see the beauty given by the lines hidden in a golden rectangle. We will see how useful golden rectangles are when we study the icosahedron.
