CALCULATING THE AREA OF A RHOMBUS
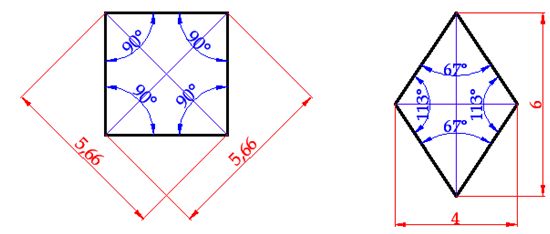
Remember that both the square and the rhombus are similar in the sense that both are parallelograms, in other words, they both have two pairs of parallel sides (equally measured). In a square, the four angle are equal. A rhombus, on the other hand, has two pairs of equal angles. The sides of a square have the same length while the rhombus has two pairs of sides which have different lengths.
You can test what you've just read in the following images:
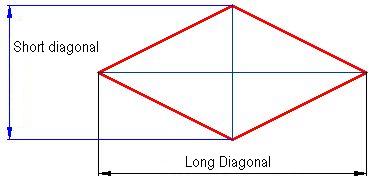
Remember that the diagonal lines in a rhombus have different lengths:
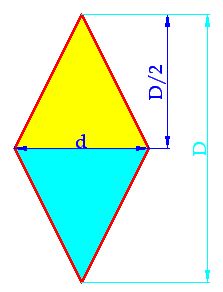
If you pay close attention, there are two equal triangles formed inside the rhombus as you can see from the image below:
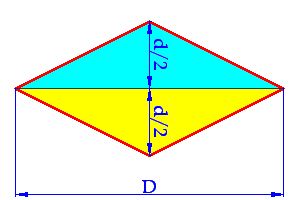
The base of the yellow triangle has a length equal to the length of the longer diagonal, and the height (or max width) equals the shorter diagonal.
We see that the area of the rhombus is calculated by multiplying both diagonals and dividing this product by 2.
We can also calculate the area of the rhombus in the following way:
If you pay a closer look to the following shape, we have two triangles forming a rhombus. Both triangles are equal. The height of each one of the triangles equals half the longer diagonal of the rhombus; and the base, common in both triangles, is equal to the shorter diagonal.
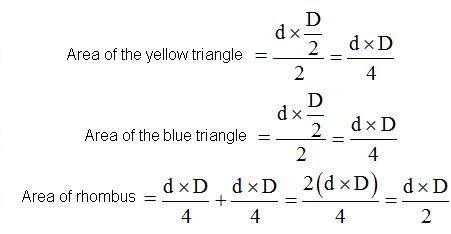
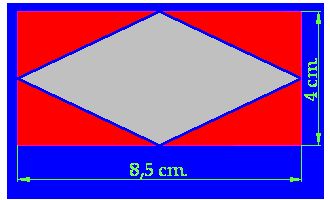
15(2).13 Calculate the red area in the following shape:
Answer: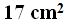 
Solution
We are going to solve this in two ways:
a) We calculate the area of the rectangle: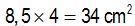 
We calculate the area of the rhombus: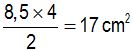 
The difference between the area of the rectangle and the area of the rhombus will give us the red area: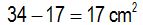 
b) If you watch the shape closely, you will notice that the red areas are triangles. Their measurements are indicated in the image:
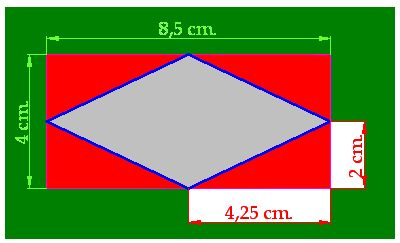
We have 4 triangles which have a base of 4,25 cm. and a height of 2 cm., in other words, each triangle has a surface of:
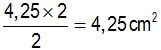
Since they are 4 triangles, the area in red is: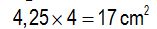
15(2).14 The area of a rhombus is equal to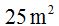
and the longer diagonal is twice as long as the shorter diagonal. Calculate the value for both diagonals:
Answer: the longer diagonal is 10 m., and the shorter diagonal is 5 m.
Solution:
If the value of the shorter diagonal = d,
the value of the longer diagonal = 2d
We deducted that the area of the rhombus is equal to:
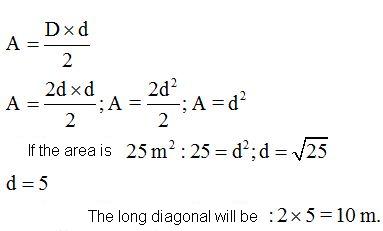
CALCULATING THE AREA OF A RHOMBOID
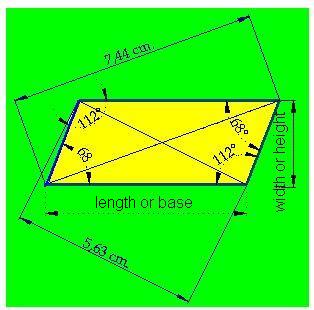
Remember that a rhomboid is a parallelogram (two pairs of parallel sides) and that it possesses two pairs of equal angles. Its diagonals are not perpendicular nor they are equal. In the following image, we have a rhomboid, with all its measurements and angles, so you can prove what we've just mentioned:
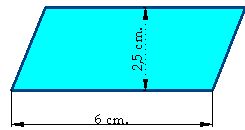
To calculate the area of a rhomboid, pay attention to the following shape:
This is a rhomboid with a base of 6 cm. long by 2,5 cm. high (or wide).
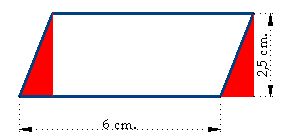
If we trace two perpendicular lines from the extremes of the upper line to its base:
We can see that two right-angled triangles have been formed (in red):
If we eliminate the first triangle and we add the second one to the rhomboid, its area will remain intact:
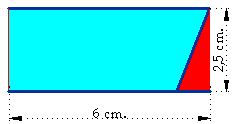
But now, it has transformed into a rectangle whose area will be its length by its height (or width).
We prove that the area of the rhomboid and the rectangle are equal. In this case: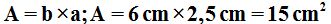 
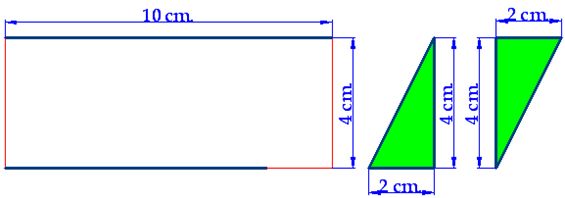
15(2).15 Take a piece of paper a ruler, a pen and a pair of scissors. Draw a rhomboid that has a length of 10 cm. and a height of 4 cm. From the extremes of the upper side, trace the heights (perpendicular lines to the base). Cut the triangles you have formed (shown in the following image in green). See if both triangles are equal. You will be left with a rectangle measuring 10 cm. long by 4 cm. wide.
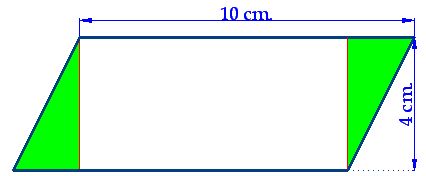
Answer:
