CALCULATING THE AREA OF A TRAPEZOID (trapezium)
A trapezoid (or trapezium) is a quadrilateral that has two parallel sides. A trapezoid is not a parallelogram. A parallelogram is a quadrilateral with two pairs of parallel sides.
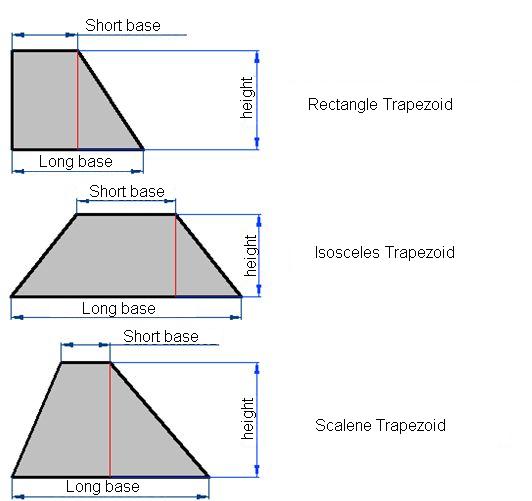
In the images below, you have three types of trapezoids:
1) Rectangle trapezoids.- They have 2 right angles (90°) and 2 parallel sides.
2) Isosceles trapezoids.- The two sides which are NOT parallel have the same length.
3) Scalene trapezoids.- Its 4 sides have different lengths and it has 2 parallel sides.
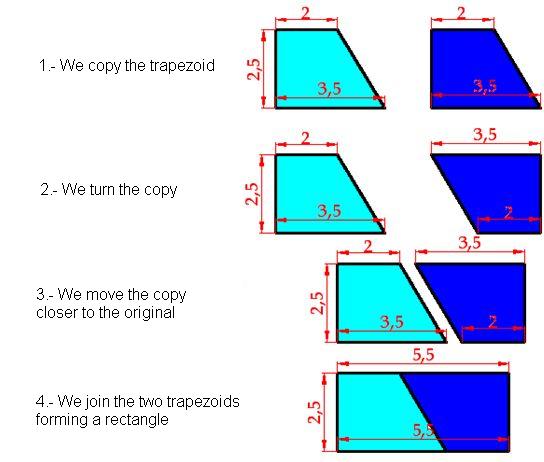
To calculate the area of a trapezoid, pay close attention to the four steps we will follow with a rectangle trapezoid:
First, draw a rectangle trapezoid.
Make a copy.
Turn the copy 180º.
Move the copy closer to the original.
Join them and you will get a rectangle whose base is the sum of the two bases.
Its height or width is still the same. Look at the steps in using the images below:
If we calculate the area of the rectangle we have formed, we have:
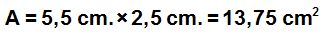
Is this the area of the trapezoid? NO, because this rectangle was formed by two equal trapezoids. Now, the area of one of the trapezoids will be:
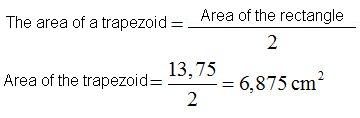

15(2).16 Draw two trapezoids that have a short base of 5 cm., a long base of 10 cm., and a height of 6 cm. Now, cut both trapezoids. Turn one of the trapezoids 180º and join them. Calculate the area of the rectangle you have formed and the area of one of the (equal) trapezoids:
Answers: 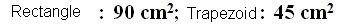
15(2).17 If instead of having used a rectangle trapezoid to calculate the area of a trapezoid, we would have used a scalene trapezoid, would the answer be the same?
Answer: Yes
Graphic Solution:
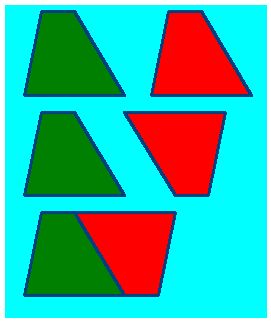
Note:
Draw a scalene trapezoid (green). Make a copy (red). Turn the copy 180º. Bring the copy and the original together. Now, we have a rhomboid whose base length equals the sum of both bases. Given that the area of the rhomboid equals that of the rectangle, calculating the area of the trapezoid is the same: half the area of the rectangle or the rhomboid by its height. Add the two bases by the height and divide this result by two (because in these cases, both the rectangle and the rhomboid contain two equal trapezoids).

