PERIMETER OF A REGULAR PENTAGON
WE call perimeter to the outer edges of a shape and since the edges of a regular pentagon are 5 equal segments, its perimeter will be the sum of all its sides. Thus, we can say that the area of a pentagon is equal to the perimeter times the apothem divided by two.
15(2).20 The perimeter of a pentagon measures 25 cm. and its area equals 50 cm2. What is the length of its apothem?
Answer: 4 cm.
CALCULATING THE AREA OF A REGULAR HEXAGON
First, draw a regular hexagon.
As you can see, there are 6 equilateral triangles (equal sides, equal angles).
We can use the same method used to calculate the area of a regular pentagon to calculate the area of a hexagon.
1st Calculate the area of a triangle multiplying its height (or the apothem of the regular hexagon) by its base (or side of the hexagon). Divide this product by 2 and multiply this result by 6 (number of sides in a hexagon or number of triangles):
We solve the area of the 6 triangles (shown in the following image):
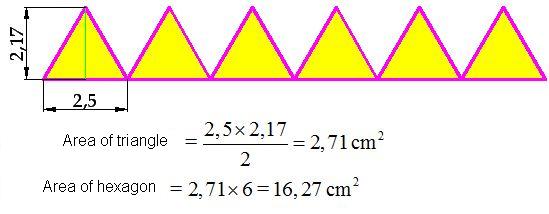
2nd Consider the hexagon as a single triangle whose base is the perimeter of the hexagon, in other words, the sum of the bases of the 6 triangles and their height (or apothem):
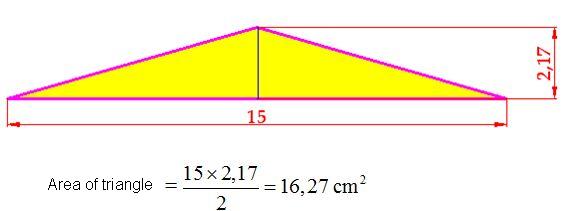
As you can see, both methods lead to the same result. Choose whichever you like.
15(2).21 How many square metres does a hexagonal park (filled with trees) have? The measurements are in the following image:
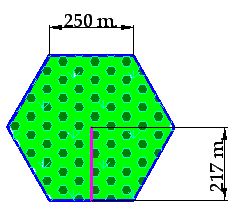
Answer: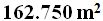
15(2).22 We want to plant some oaks in a lot full of stones by the mountain. Each plant needs a space of 6 square metres of land. How many plants do we need taking into consideration the shape and dimension of the lot (shown in the following image)?
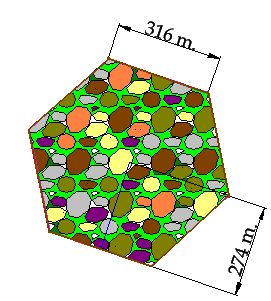
Answer: 43.292 oaks.

