CALCULATING THE AREA OF A CIRCLE.
We continue using the same method for calculating the area of shapes without having to memorize any formulas.
Draw a circumference with a radius of 3,5 cm.
Cut the piece of paper using the line you just drew, in other words, cut the circumference and when you are done , you will have a circular surface or a surface / part of a plane (piece of paper) limited by a circumference.
Can we consider the circumference as a multiple-sided polygon?
Of course we can! Let's see how we do this.
Draw a circumference with a radius of 3,54 cm.
Inside the circumference, draw 20 triangles using the measurements you see in the image below:
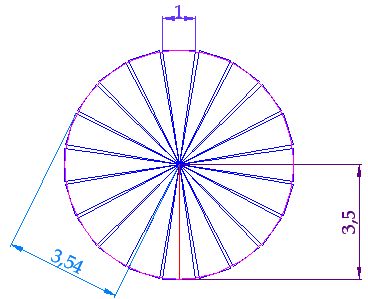
The sum of the bases of the 20 triangles barely coincide with the radius of the circumference.
We have taken a section of the image above and we have doubled its size:
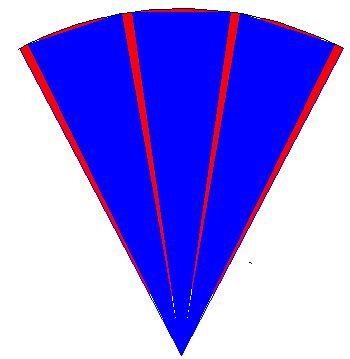
You can see the surface of three triangles in a larger scale in blue from the image above it. You can see the surface we haven't covered in red. This means that the area of the circle will be greater than that of the sum of all the triangles. The area of the circle will be equal to the sum of all the triangles plus the surfaces in red.
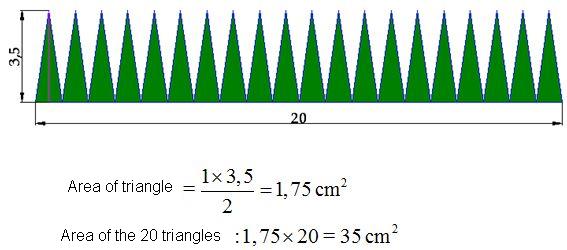
Calculate the area of the 20 triangles:
It would be the same to merge all the triangles into one:
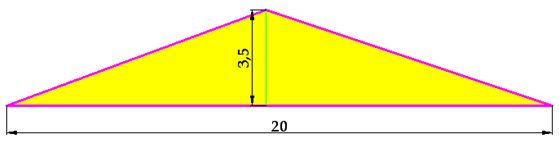
These 20 triangles can be merged into one using the sum of all their bases as the single base. Their height is common in all of them.
Its area is:
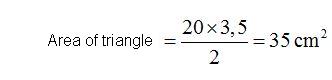
If we were to use triangles with smaller bases inside the circle, they would be closer to the line of the circumference. This means that the total area of all the triangles would be closer to the surface of the circle.
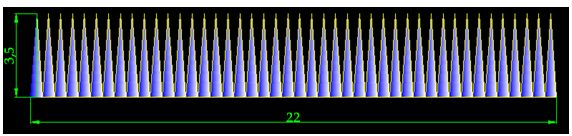
Instead of drawing 20 triangles with a base of 1 cm. and a height of 3,5 cm., we will try with 44 triangles with a base of 0,5 cm. and the same height of 3,5 cm:
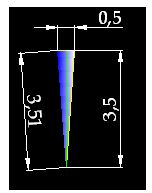
You can see the result in the following image. We have 44 triangles with a height of 3,5 cm. with a base of 0,5 cm. inside the circumference:
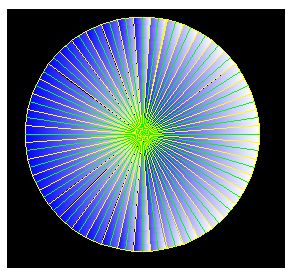
As you can see, by making better use of the space between one triangle and the next (comparing 20 triangles against 44 triangles), the measured surface has increased from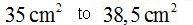 
Now, the line formed by the 44 triangles are closer to the circumference. They are more exact than when we used 20 triangles with a base of 1 cm.
How do we calculate the area of a circle exactly?
In the case of the 44 triangles, the sum of all their bases would have a value of: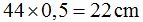 
and their height would be the same, 3,5 cm.
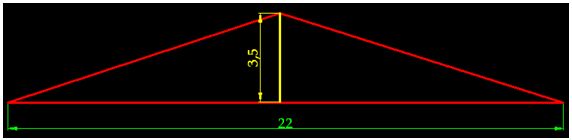
We transform the previous shape into a single triangle, using its surface:
The area of this triangle is: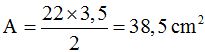 
In spite of having increased the number of triangles to 44, their bases do not form a perfect curve. There is still a small difference (as you can see from the image below - image has been doubled 8 times):
As you can see, the white lines do not match the red ones. This means that the area of the circle is higher than that of the 44 triangles.
How do we calculate the area of the circle?
In a very simple way. In the case of the 44 triangles, we have calculated that the perimeter, in other words, the sum of their is 22 cm.
Instead of using the perimeter of the 44 triangles as base, we take the length of the circumference, which we know is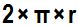 
, as a perimeter or base length. However, we don't have to take the height of the triangle but the radius of the circumference into consideration, which is the side of the triangle. It measures 3,51 cm.:
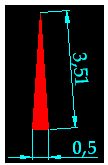
Its height is the perpendicular line to the base of the triangle and the side of the triangle will be longer than its height. Now, we have a triangle with a base of 3,51 cm. and a height of 3,51 cm.
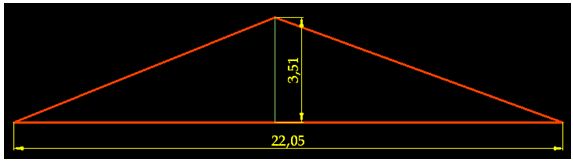
The exact area of the circle is a height of 3,51 cm. and a base of 22,05 cm.:
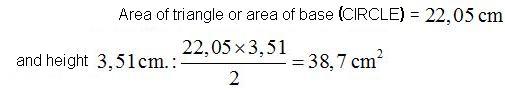
You will find a small difference between calculating the area of the circle using the triangles and calculating it by using as base of the SINGLE triangle the length of the circumference and the radius or one of the sides of the triangle:
The difference is: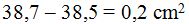 
When you have to calculate the area of a circle, you may do so considering it as a triangle in which its base is the length of its edges or circumference and the height is the value of its radius:
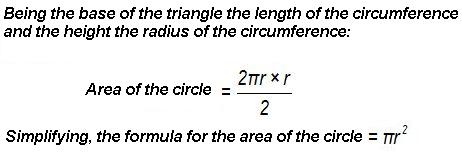
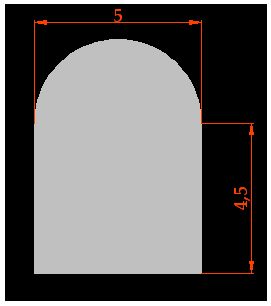
15(2).23 Calculate the area of the shape in gray. The measurements are shown in the image:
Answer: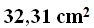 
Solution:
We have a semi-circle with a radius of 2,5 cm. (half the diameter, which is 5 cm.) and a rectangle measuring 5 cm. long by 4,5 cm. high:
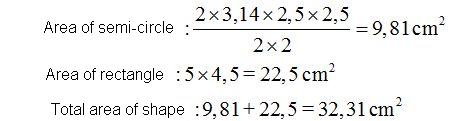
15(2).24 In the following image, you have a garden. Take into consideration the following parts and measurements (in metres):
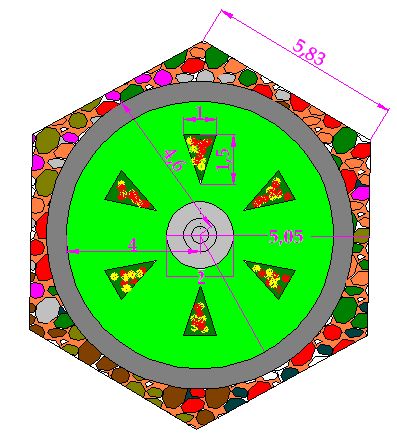
1.- The outer part has the shape of a hexagon. It is filled with flat cobblestones.
2.- A circular walkway (in gray).
3.- A lawn area or grass (in green).
4.- 6 small triangular surfaces with red and yellow rosebushes over the lawn.
5.- A central water fountain (in gray).
What is the surface of:
a) The cobblestone
b) The circular walkway (gray)
c) The lawn
d) The rosebushes
e) The central fountain?
Answers:
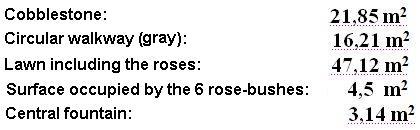
Lets test it:
If the entire garden were a hexagon, its surface would be:
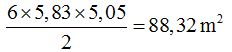
If we subtract the outer circle that forms the walkway from the hexagon, we would get the area of the cobblestone:
Area of outer circle (walkway):
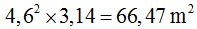
If we subtract the area of the outer circle from the hexagon, we would get the area of the cobblestone:
Lets find the area of the inner circle that forms the walkway:
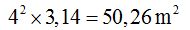
The difference between the two circles that form the walkway will give us the area of the walkway (in gray):
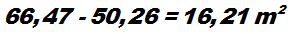
If we subtract the area formed by the fountain from the area formed by the inner circle of the walkway, we will get the area of the lawn (including the 6 rosebushes):
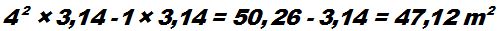
Area of the 6 rosebushes:
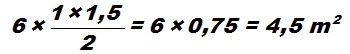
Area of central fountain:
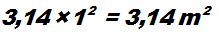
The sum of the cobblestone plus the area of the circular walkway plus the area of the lawn (including the 6 rosebushes) plus the area of the fountain: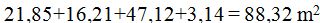 
, as you can see, it matches the area we calculated if we considered the garden as a hexagon.
