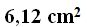CALCULATING THE AREA OF A CIRCULAR CROWN
We call a circular crown to the part composed by two circumferences that possess the same centre:
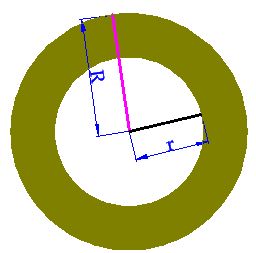
The coloured area in the image above is the circular crown.
To know its surface, we need to know the measurements of the major radius (R) and the minor radius (r).
First, we calculate the area of the circle with the major radius (R). Then, we find the area of the circle with the he minor radius (r) and we calculate their difference. This difference represents the circular crown:
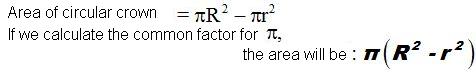
As you can see, we find the difference of the squares of the radii and we multiply by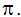 
15(2).25 Find the area for the region in red for the following image (in centimetres):
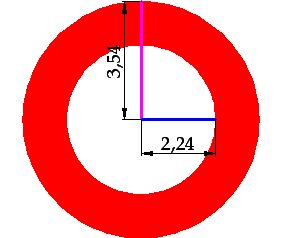
Answer: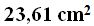 
CALCULATING THE AREA OF A CIRCULAR SECTOR
First of all, we need to know what a circular sector, zone, portion, part, etc. is.
It is simply a part or zone of a circle which is composed by TWO RADII AND THE ARCH composed by both of them.
You will find that it is a simple concept after testing the following figure:
The circular sector is the surface of the circle composed by two radii and the arch.
To calculate the area, we simply need two pieces of information; the length of the radius and the angle formed by both radii.
We can get the result with a simple rule of three:
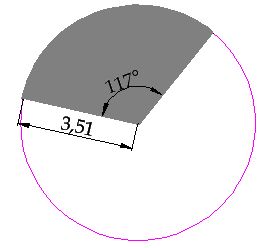
15(2).26 Calculate the surface of the circular sector which corresponds to the previous image:
Answer: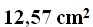 
Solution
If 360 º corresponds to a surface of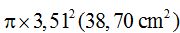 
, 117º will correspond to a surface of 
.
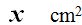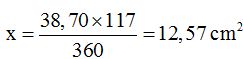
15(2). 27 Calculate the area of the circular sector whose central angle is 60º and whose radius has a length of 5 cm.
Answer: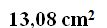 
CALCULATING THE AREA OF A CIRCULAR TRAPEZOID
First, we need to know what a circular trapezoid is. It is a regular trapezoid whose bases are curved.
Look at the following shape:
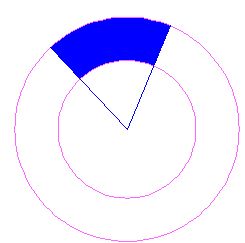
The area in blue represents the circular trapezoid. As you can see, its bases are curved.
To calculate the area of the surface in blue, we need to find the area of the outer circle (represented by an R). Then, we need to find the area of the inner circle (represented by an r). We find their difference and we get the area of the circular crown:
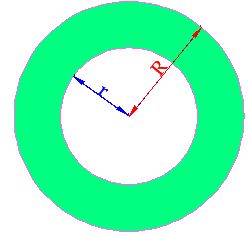
The coloured zone is the area of the circular crown which corresponds to a central angle of 360º.
When calculating the area of a circular trapezoid, we need to know the area of the circular crown which corresponds to a specific angle, as you can see in the following image:
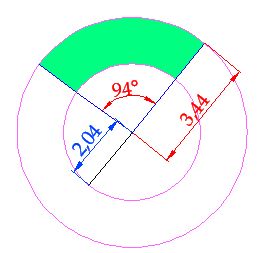
15(2).28 Calculate the coloured area for the previous image, taking into consideration the information shown in it (in centimetres).
Answer: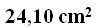 
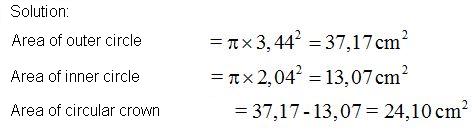
The calculated surface corresponds to 360º. Now, we need to calculate the surface corresponding to 94º.
We'll use the rule of three to do this:
If 360 º corresponds to a surface of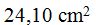 
,
94º will correspond to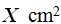 
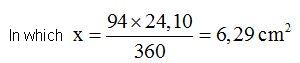
15(2).29 Calculate the area of a circular trapezoid whose measurements are: R = 3 cm., r = 1,5 cm., and a central angle of 104º.
Answer: 
