PARENTHESIS, BRACKETS AND KEYS.
So far, we have used parentheses (...) and brackets [...] to separate specific operations. Remember that you have done several exercises with them: for example: 2[2+(3+6)-12]
For one parenthesis you open, there must be another one to close it. You also need to do this with brackets and keys.
Sometimes, we have the need to separate manu operations in the same exercise. We use keys {...} to cover these need. Keys work in the same way as parenthesis and brackets; they separate values.
If you have parentheses, brackets, and keys in the same exercise, you must start with the operations between parenthesis, then, solve the ones in brackets, and finally those operations inside keys. For example:
a) 2 {[3+2 (4-3)-2 (6-8)-5]} = 2 {[3+2 1-2 (-2)-5]} =
= 2 {[3+2+4-5]} = 2 {4} = 8
b) 3{4(2-7)-11-2[3(-5-1)]} = 3{4 (-5)-11-2[3 (-6)]}=
= 3{-20-11-2[-18]} =3{-31+36} = 3{5} = 15
Try to solve these three exercises on your own:
a) -3(4-6)-2{5[3-5(-7+5)-3]} the answer is: -94
b) -3{-4[-5(-6 x2-7)]} the answer is: 1140
c) 4-2{3[5-2(5-6)-7]+10}+17 = the answer is: 1
In case you've had any problems, here are the solutions:
a) -3 (-2)-2{5[3-5 (-2)-3]} = 6-2{5[3+10-3]} =
= 6-2{5 (10)]} = 6-2{50} = 6-100 = -94
b) -3{-4[-5(-6x 2-7)]} = -3{-4[-5(-12-7)]} =
= -3{-4[(-5 (-19)]} = -3{-4[95)]} =
= -3{-4 95} = -3{-380} = 1140
c) 4-2{3[5-2(5-6)-7]+10}+17 = 4-2{3[5-2(-1)-7]+10}+17 =
= 4-2{3[5+2-7]+10}+17 = 4-2{3 0+10}+17=
= 4-2{0+10}+17 = 4-2 10+17 = 4-20+17 = 21-20 = 1
Exercises
A) A person receives a monthly salary of 1400 € and another person, 48 € a day. What is the difference between the total amounts received by each person at the end of the year?
Answer: 720 €
Solution:
The first person will receive in a year: 1400 x 12 = 16800
In a 365 day year, the second person will receive: 365 x 48 = 17520
The difference, in favour of the second person, is: 17520 – 16800 = 720
B) One car has ran 515 kilometres in 5 hours. Another car has traveled 749 kilometres in 7 hours. After having traveled for 10 hours, how many kilometres has each car covered?
Answer: The first one has traveled 1030 km. and the second, 1070km.
C) Two people work together in a construction site. The first one earns 5 € a day more than the second person. After several work days, the first one earned 450 € and the second person, 400 €. 1) How many days did they work? and 2) What is their daily wager?
Answers: 1) They worked for 10 days. 2) Their daily wagers are 45 and 40 €
Solution:
The exercise states that the first worker earns 5 € a day more than the second one.
After working for several days, the first one earns 450 € and the second one earns 400 €. This means that during the days they have worked, the first one earns: 450 – 400 = 50 € more than the second worker.
If the first one earns daily 5 € more than the second worker, we could deduct the amount of days they have worked. We simply divide:
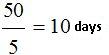
If the first one has earned 450 € and the second 400 €, their wager (the total they have earned per day) will be:
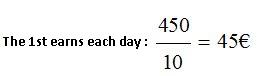
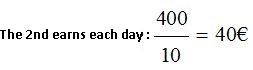
D) Three friends decide to weight themselves. The first and second weighed 143 kilos combined; the second and third weighed 145 kilos combined; the first and third weighed 144 kilos combined. How much does each one weighs?
Answer: the first one 71 kilos, the second 72 kilos, and the third 73 kilos
This exercise isn't easy, so we will explain it. Try to understand it correctly.
Solution:
Before we begin solving it, lets explain a couple of things:
1) We can add and subtract anything that is homogeneous (of the same species), for example: bags of potatoes with bags of potatoes; kilos of onions with kilos of onions; Euros with Euros, etc.
Example: 5 bags of potatoes + 4 bags of potatoes = 9 bags of potatoes.
3 Euros + 9 Euros = 12 Euros.
2 first positions + 4 first positions = 9 first positions.
2 times the first one + 6 times the first one = 8 times the first one
2) If they ask us to divide ( 4 + 8 + 12 ) into two:
We have to divide each one of its segments, parts or terms:
4:2 +8:2 + 12:2
It is the same to add: 4 + 8 + 12 = 24 and then to divide it by 2; 24:2= 12;
to add the quotients of 4:2 +8:2 + 12:2 = 2 + 4 + 6 = 12
Following what was stated in the exercise, we can write:
the first one + the second one = 143
the second one + the third one = 145
the first one + the third one = 144
If we add all of them, we have:
the first one + the first one + the second one + the second one+ the third one + the third one = 143 + 145 + 144
We have: the first one two times + the second one two times + the third one two times = 432
The word "times" means multiply: for example, 4 times 3 = 12
The previous sum: the first one (1°) + the first one + the second one + the second one+ the third one + the third one = 143 + 145 + 144
We could write it: 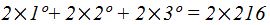
We divide each term by 2 (because each segment is in the exercise twice) and we get: 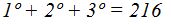
We know that the first one + the second one + the third one = 216; and the first one + the second one = 143
If we subtract both expressions, we can calculate the weight of the third friend:
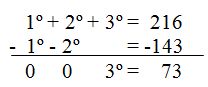
We find out that the third friend weighs 73 kilos.
We know that the first one + the second one + the third one = 216; and the second one + the third one = 145
If we subtract both expressions, we can calculate the weight of the first friend:
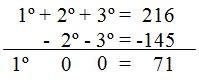
We find out the the first friend weighs 71 kilos.
We know that the first one + the second one + the third one = 216; and the first one + the third one = 144
If we subtract both expressions, we can calculate the weight of the second friend:
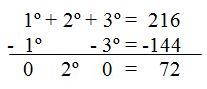
We find out that the second friend weighs 72 kilos.