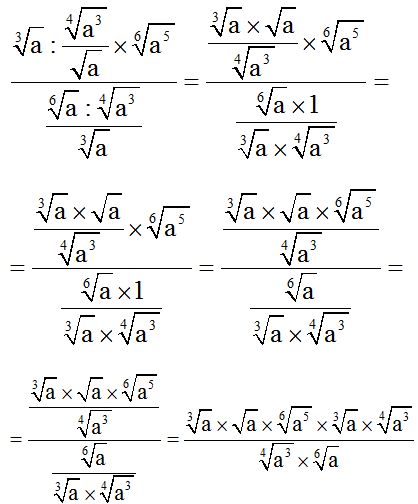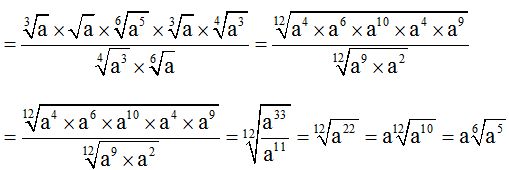Reducing to a Least Common Multiple of Indices.
We will sometimes have to multiply or divide radicals with different indices. Whenever these are equal, we can multiply or divide them with no problem:
10.68 Multiply: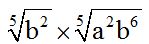 
Answer: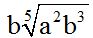 
Solution:
Here you have it solved step-by-step:
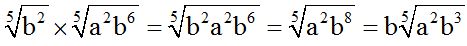
10.69 Calculate the quotient of:
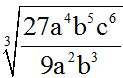Answer: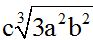 
When indices are different, we calculate their l.c.m.. This value is divided by each one of the indices and the quotient is multiplied by each one of the exponents of the radicant.
10.70 Multiply: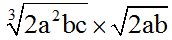 
Answer: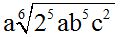 
.
Solution:
The indices are 2 and 3. The l.c.m. (2 and 3) = 6
When we divide 6 by 3, we get 2 as quotient. This quotient is multiplied by the exponents of each one of the factors of the radicant of the multiplier.
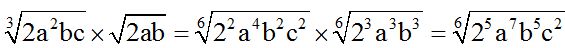
Always bring out any factor you can from the radical:
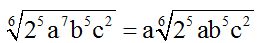
10.71 Multiply: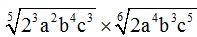 
.
Answer: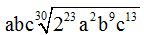 
10.72 Divide:
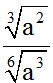Answer: 
.
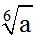Solution:
We calculate the l.c.m. (3 and 6) = 6. We divide the l.c.m. by each index. The resulting quotient is multiplied times each exponent we have in the radicant. Then, we reduce (simplify) any similar terms if any. Finally, we divide the numerator by the denominator bearing in mind that to divide exponents with the same base, we subtract the exponents:
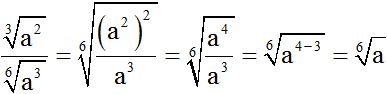
10.73 Calculate:
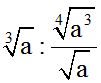Answer: 
.
Solution:
We just have to keep in mind what we've studied so far about dividing fractions, dividing powers and radicals.
Here, you have a way of solving the exercise:
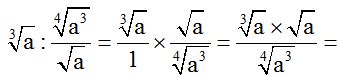
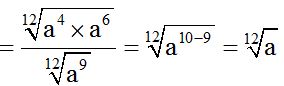
10.74 Find the value of:
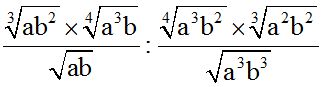Answer: 
.
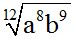Solution:
Here, you have a way of solving the exercise, step-by-step:
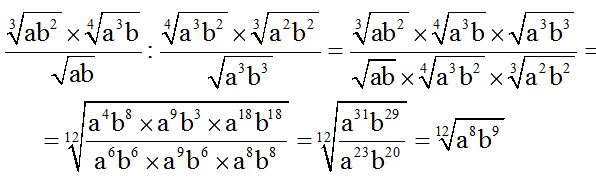
10.75 Calculate:
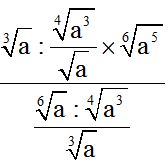Answer: 
.
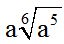Solution:
One way of solving this can be the following:
