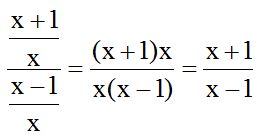Multiplying and Dividing Algebraic Fractions.
We simply need to remember how fractions are multiplied or divided, as we have studied so far. We need to bear in mind, in regards to literal variables, that to multiply powers with the same base, we add the exponents and when we divide, we must subtract the exponents.
10.21 Calculate:
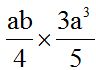Answer: 
.
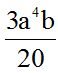Solution:
To multiply fractions, we calculate the numerators and we divide by the product of the denominators. If possible, we simplify any common factors:
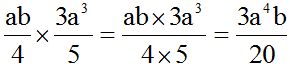
10.22 Calculate:
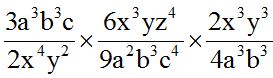Answer: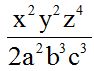 
Solution:
We multiply the numerical part first. Then, we work on the literal part (letter variables) adding the exponents of the powers of the same base:
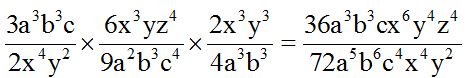
We divide the numerical part first and the the literal by subtracting the exponents of the powers of the same base. We write the result wherever the exponent was the highest:
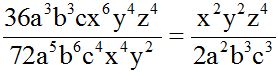
10.23 Calculate:
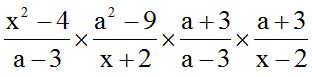Answer: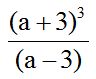 
Solution:
We indicate products and simplify common factors :
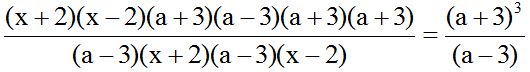
10.24 Calculate:
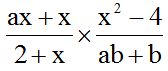Answer: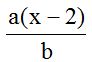 
Solution:
Before working on the product, check each term in the numerator and denominator to see if there are any common factors to simplify. This will help you work with smaller values.
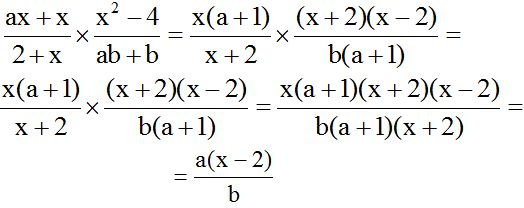
10.25 Calculate:
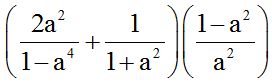Answer: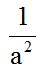 
Solution:
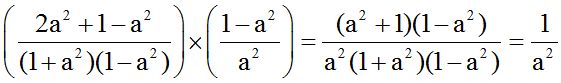
10.26 Calculate:
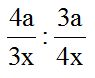Answer: 
.
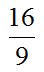Solution:
Remember that to divide fractions, you can multiply the first by the inverse of the second. In other words, we can "turn around" the second fraction. This is the same as placing the numerator as a denominator and the denominator as a numerator.
We can also multiply the first numerator by the second denominator. We divide this product by the product of the first denominator times the numerator of the second fraction.
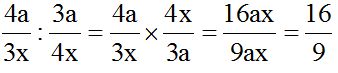
10.27 Calculate:
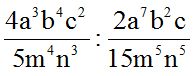Answer: 
.
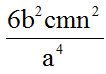10.28 Calculate:
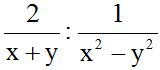Answer: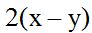 
Solution:
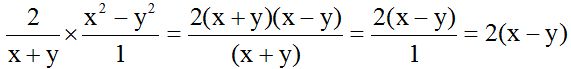
10.29 Calculate:
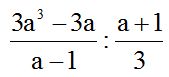Answer: 
Solution:
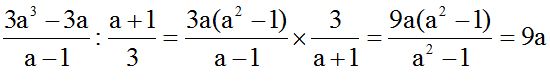
10.30 Calculate the quotient:
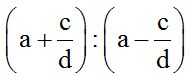Answer: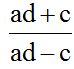 
Solution:
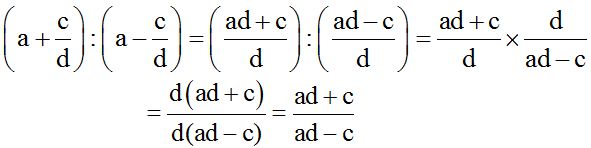
10.31 Calculate:
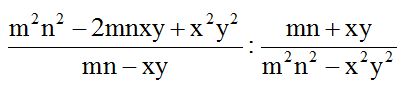
Answer: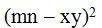
Solution:
We solve this having factoring products in mind: the square of the difference of two numbers and the sum of two numbers times their difference is equal to the difference of its squares.
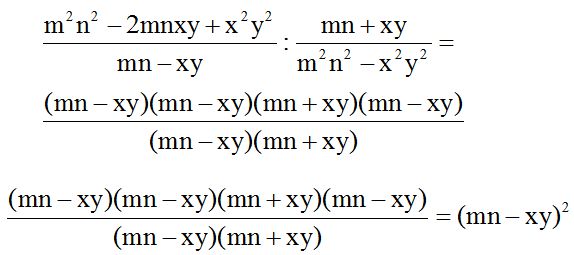
10.32 Calculate :
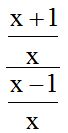Answer: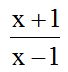 
Solution:
Whenever you face a fraction divided by another fraction of this type:
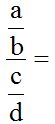it is the same as: 
.
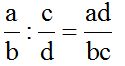In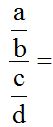 
, the extreme terms are ‘a’ and ‘d’ (1st. and 4th.) and the middle terms are ‘b’ and ‘c’
This procedure is very simple;
The product of the extreme terms divided by the product of middle terms:
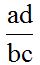
If we apply this to our exercise, we have:
