TIME ZONES.
However, what we've just studied about time zones doesn't apply in practice.
Some countries found in different meridians decide to have the same time zone because of country boundaries, regions, agreements, etc. Such is the case, as we mentioned before, of the EU (European Union) where countries belonging to this union have taken the same time zone (except for Portugal and the U. K.). To help make this point clearer, pay attention to the following image:
Map with the different time zones:
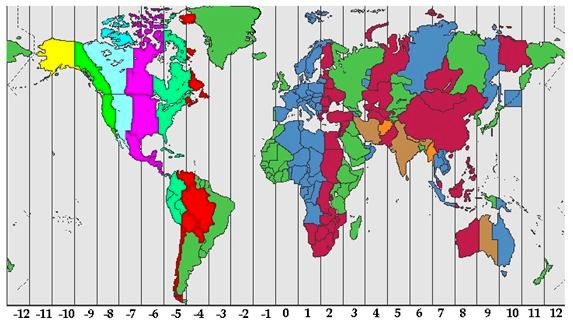
The countries you see in the same colour (vertically) correspond to the same time zone, regardless of the meridian they are in.
15(4).18 When it is 4 p.m. in Spain, what time is it in Sydney (east coast of Australia)?
Answer: 1 a.m. the next day
Solution
If you pay attention to the previous image, you will see that Sydney is found at 9 spherical caps to the right of Spain. This corresponds to 9 hours later in the Australian city. In other words, 1 a.m. of the next day.
15(4).19 When it is 2 a.m. in Spain, what time is it in the capital of Chile, Santiago?
Answer: it's 8 p.m. of the day before
Solution
If you pay attention to the previous image, you will see that Santiago is found at 6 spherical caps to the left of Spain. In other words, 6 hours less, which equals to 8 p.m. of the previous day in Santiago.
15(4).20 When it is 12 o'clock (noon) in Spain, what time is it in Tokyo, the capital of Japan?
Answer: it's 8 p.m. of the same day
Solution
Japan is found at 8 spherical caps to the right of Spain. Thus, it will be 8 p.m. of the same day
15(4).21 When it is 10 a.m. in Spain, what time is it in Reykjavik, capital of Iceland?
Answer: it's 9 a.m. of the same day
SPHERICAL ZONES.
In 15(3), as you remember we studied the spherical zone as an intersection of two parallel planes with a sphere.
Deducing the area of the spherical zone is not an easy task.
Following the footsteps of great geniuses, like Archimedes (250 b.c.), who told us that the surface of a spherical zone, which corresponds to a sphere with a radius R and a distance h between the two parallel planes that cut the sphere, is equal to the surface of a cylinder with the same radius R and a height h.
Let's see the following image:
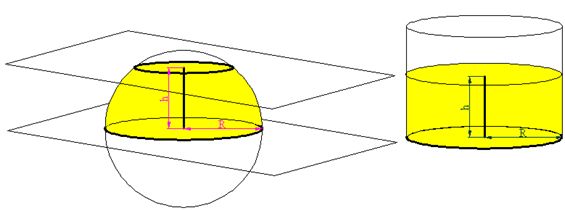
To the left, we have the section of the sphere after being cut by 2 parallel planes (perpendicular to their vertical axis).
To the right, we have a cylinder with the same radius and the same height. In yellow, you can see the surface of the cylinder corresponding to the side area of the cylinder with a radius R and height h.
Calculating the side surface of the cylinder is very simple. We know it is equal to multiplying the base times the height.
Since the base is a circumference with radius R and height h, the area will be:
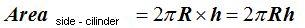
And the area of the spherical zone, with a radius R and a height between both parallel planes h, will be the same,
In other words,
You can test this using a sphere with a rough surface. After fixing the thread, place it around the sphere anywhere you like, as seen in the following image:
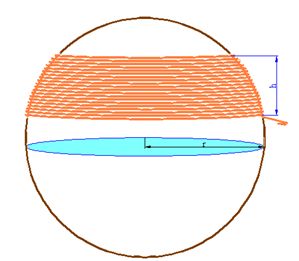
Once you have wrapped the thread around the surface of the sphere (with an approximate height of 3 to 4 cm.), remove the thread you used (the amount used to cover the 3 or 4 cm.). Now, use that same amount of thread in a tube or cylindrical bottle with the same radius as the previous sphere, wrap it again as you see in the following image:
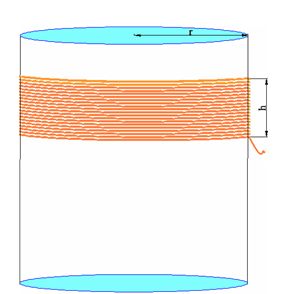
You will find out (once you finish wrapping the cylinder using the same amount of thread you used on the sphere) that it has the same height as the spherical zone. Now, we can safely conclude that both surfaces, the spherical sphere and the cylinder, are equal.
From this observation, and thanks to Archimedes, it becomes easier to calculate the area of a spherical zone, using the side area of a cylinder.
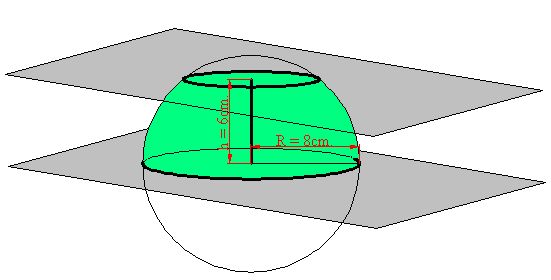
15(4).22 Calculate the area of a spherical zone of 6 cm., high. The radius of the sphere has a value of 8 cm. Draw the shape.
Answer: 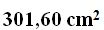
The shape could be: