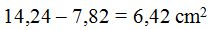CALCULATING THE AREA OF A CIRCULAR SEGMENT
First, we have to know what a circular segment is.
This refers to the surface of a circle which is limited by a chord (a geometric line segment which ends in any two points on the circumference) and the arch it forms:
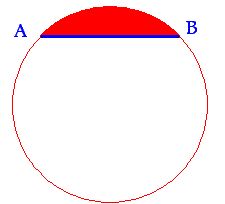
The chord is the 
segment and the arch is the length of the circumference between points A and B.
The circle zone (in red) is the surface we call circular segment area.
How do we calculate this circular segment area?
This is a very simple procedure taking into consideration what we have learned so far:
1) We draw a circumference, an arch, the chord and one of its extremes with the centre of the circumference:
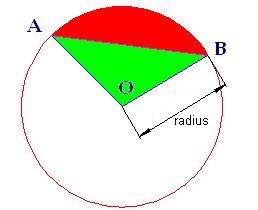
2) I calculate the area of the circular sector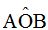 
and then the area of the triangle (in green) .
3) I find the difference between both areas and this result will be the area of circular segment AB.
15(2). 30 Calculate the area of the circular segment of the shape you have in the following image. The measurements are represented in centimetres:
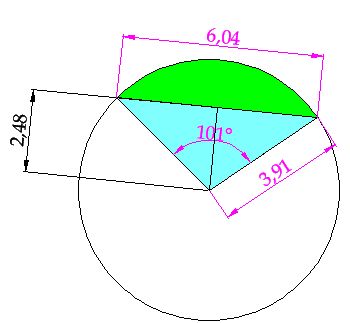
Answer: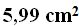 
Solution
1) Area of the circular sector:
If 360 º corresponds to an area of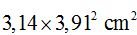 
,
101º will correspond to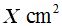 
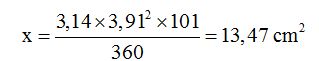
2) Triangle area:
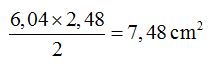
3) Area of circular segment:
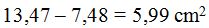
15(2). 31 Calculate the area of the circular segment of the shape you have in the following image. Its measurements are: a sagitta measuring 0,62 cm., (a sagitta is a segment that joins the middle point of the arch with the middle point of the chord), a radius of 2,92 cm., and an angle of 76º for the circular sector.
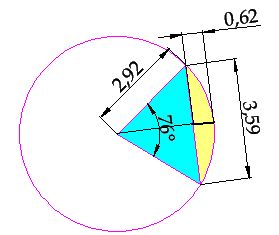
Answer: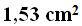 
Solution
1) Area of the circular sector:
If 360 º corresponds to an area of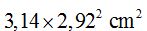 
,
76º will correspond to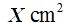 
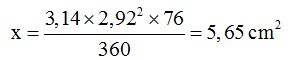
2) Triangle area:
I must know the height. To do that, I calculate the difference between the radius and the sagitta: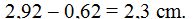 
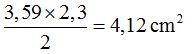
3) Area of circular segment: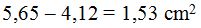 
15(2). 32 Calculate the area of the circular segment (in red) for the figure you have in the following image. Its measurements are: a radius of 4 cm., a triangle base of 6,23 cm.(in blue), and an angle of 102º for the circular sector.
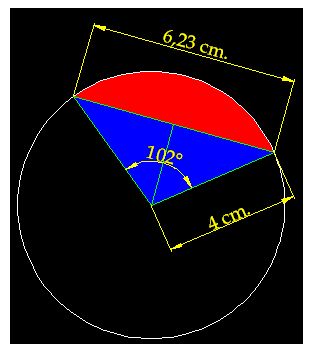
Answer: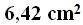 
Solution
1) Area of the circular sector:
If 360 º corresponds to an area of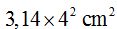 
,
102º will correspond to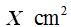 
2) Triangle area:
To calculate its height, I use the Pythagoras theorem. The height is a cathetus and half the base, (since it is an isosceles triangle - two equal sides are radii or radiuses) the other cathetus, and the hypotenuse.
Remember that the sum of the squares of the catheti is equal to the square of the length of the hypotenuse.
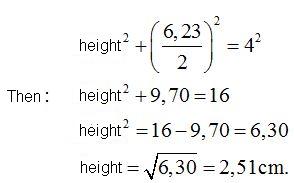
I know the base and height of the triangle. Its area will be:
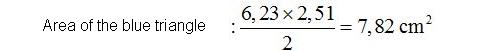
3) Area of circular segment:
