CALCULATING THE AREA OF A TRAPEZOID
Remember that a trapezoid is a quadrilateral, in which only two of its sides are parallel to one another, thus, it is not a parallelogram. As in any quadrilateral, the sum of its angles equals 360º. The length of its sides is different as well as its angles and diagonals:
The area of a trapezoid will be studied under trigonometry.
CALCULATING THE AREA OF A REGULAR PENTAGON
First, draw a regular pentagon:
Remember that a regular polygon is that which has equal sides (as a result, its angles will also be equal). Join the centre of the pentagon with each vertex:
As you can see, we have formed as many triangles as the sides on our polygon:
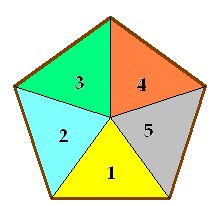
Trace the height of one of the triangles, which is also the apothem of the polygon:
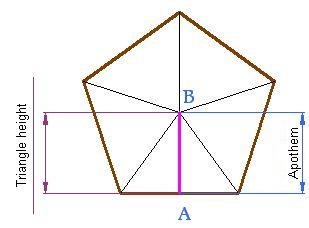
Cut the hexagon you have drawn. You now have in your hands a hexagonal surface.
There are two ways to calculate the area of a regular polygon, in this case a pentagon:
1.- Calculate the area of a triangle and multiply this result by 5 (the number of triangles in the pentagon):

2.- We could consider the pentagon as a single triangle which has as base the total sum of the bases of each one of the triangles that form it and a height equal to the value of the apothem:

To prove this, we will calculate the area of the regular pentagon using both ways we've just studied.
15(2).18 Calculate the area of the pentagon:
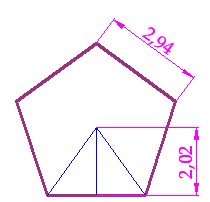
Answer: 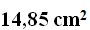
1st Solution:
The area of one of the triangles is:
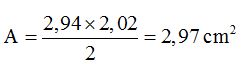
Since they are 5 triangles, the area will be: 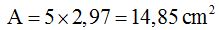
2nd Solution:
The total base would be:
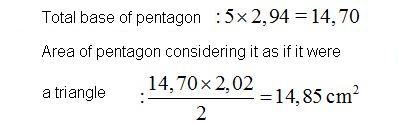
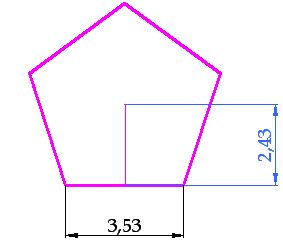
15(2).19 Calculate the area of a pentagon shown in the image below using both methods. Prove that both results are exactly the same:
Answer: 

